TRIVIUM: 密码学 Stream Cipher

Trivium 加密算法实际上是一个优美的硬件数字电路.

Introduction

之前一篇文章介绍了最近 50 年的 现代密码学：对称加密，非对称加密，和加密协议。

其中，非对称加密有非常完整的理论支撑，但是运行速度却远远慢于对称加密，所以通常只用非对称加密 (Asymmetric Encryption) 生成密钥对，大量数据的加密则由对称加密 (Symmetric Encryption) 完成。

我对嵌入式硬件比较感兴趣，对低成本的物联网 (IoT) MCU 而言，大量数据的加密也依赖于对称加密，例如 RFID 卡就需要高效、轻量级的对称加密算法。

• 密码学 (Cryptography)

  • 对称加密 (Symmetric Encryption)

    • 流加密 (Stream Cipher)
    • 块加密 (Block Cipher)

  • 非对称加密 (Asymmetric Encryption)

    • 整数分解 (Integer Factorization)
    • 离散对数 (Discrete Logarithm)
    • 椭圆曲线 (Elliptic Curve)
    • 格密码 (Lattice Based)

  • 加密协议 (Protocols)

    • 数字签名 (Digital Signature)
    • 消息认证 (Message Authentication)
    • 密钥制定 (Key Establishment)

对称加密又分为 流加密 (Stream Cipher) 和 块加密 (Block Cipher)。从名字来看大概就能猜到，Stream Cipher 是以数据流的形式，一个 bit 一个 bit 地加密数据的，而 Block Cipher 则是把数据分块，一块一块地加密的。之后会分别以轻量级的 Trivium (流加密) 和 Present (块加密) 为例，分别介绍 Stream Cipher 和 Block Cipher。

这篇文章则专注于 Trivium Stream Cipher，后面介绍的 Trivium 软硬件实现 (Verilog / C / Python) 都放在了这个 GitHub 仓库里：

• GitHub - Trivium Stream Cipher

Stream Cipher

这里用一个非常简单的例子介绍一下什么是流加密 (Stream Cipher)。例如我们希望加密字符串 ‘hi’，那么先把它翻译成二进制，‘h’ 在 ASCII 码表对应 0x68 (0110 1000)，‘i’ 在 ASCII 码表对应 0x69 (0110 1001)，那么连在一起，我们要加密的就是比特流 0110 1000 0110 1001。

那么怎么加密呢？非常出乎意料的简单，那就是用加法，不过是二进制的加法（按位加法，不考虑进位）。0+0=0，0+1=1，1+0=1，1+1=0。如果你仔细观察，会发现这加法其实就是异或运算 (XOR)，两个数不一样的时候，输出 1，相同则输出 0。

众所周知，异或运算 (XOR) 又用 ⊕ 表示，因为它就是二进制按位加法。我们把 ‘hi’ 用二进制数表示之后，再生成一样长度的二进制数，两个一起做加法就完成了加密。

例如我们要加密 1000 (plaintext)，生成一样长度的二进制数 0101 (keystream)，两者做加法 (异或运算)，1000 ⊕ 1111 = 0111 (cipher)，就成功加密了。

那么我们怎么解密呢？很简单再做一次加法。比如上面我们把 1000 (plaintext) 和 1111 (keystream) 相加，得到了 0111 (cipher)，我们把 0111 (cipher) 再和 1111 (keystream) 相加一次，就发现 0111 ⊕ 1111 = 1000 (plaintext) 我们又还原了，这样就完成了解密。

加密：1000 (plaintext) ⊕ 1111 (keystream) = 0111 (cipher)

解密：0111 (cipher) ⊕ 1111 (keystream) = 1000 (plaintext)

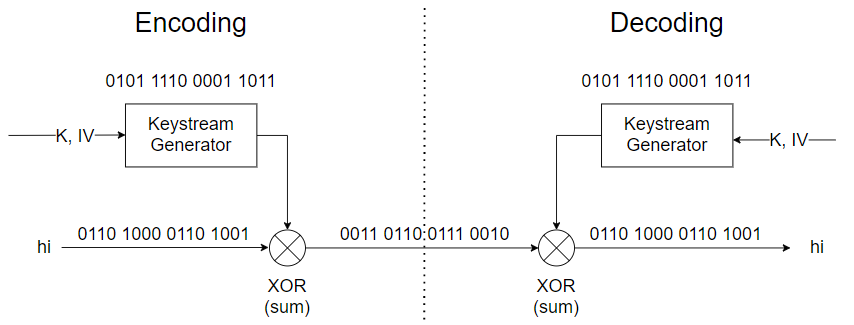
上面这张图解释了我们怎么用 Stream Cipher 加密和解密：在左边先把 hi 转换成二进制，做加法加密得到密文；在右边对密文再做一次加法，就解密又得到了 hi。

那么问题来了，我们怎么能保证左右两边生成的 Keystream 一模一样呢？这就是 Stream Cipher 的核心了，我们要保证左右两边能生成相同的 Keystream，并且 Keystream 的顺序是不可预测的，不然攻击者猜到 Keystream 就能破解密文了。

所以 Trivium 的核心就是如何安全地生成一连串的 Keystream。

Trivium Stream Cipher

下面我们详细介绍 Trivium 的算法细节。这里再次提醒，Trivium 实际上是个数字电路，由 3 个 Non-Linear Feedback Shift Register (NLFSR) 连在一起的电路。

首先，我们有一个 Trivium 机器，他的内部状态由 288 个 bit 决定 ，确定了这 288 个 bit，我们就可以复制一个 Trivium 机器，输出一模一样的 Keystream ( $Z_i$ ) 用来加密。

下面就是一组公式，决定了怎么计算 $Z_i=T_1 \oplus T_2 \oplus T_3$，其中 就是输出的 Keystream。如果把它当作公式和算法，会很难理解 Trivium，不知道这公式都是啥意思，但是把它当作一个电路来看，就豁然开朗。

下面这张图非常清晰地描述了 Trivium 的内部结构，这张图其实是个电路原理图。第一眼看上去可能会很混乱，我们对照着算法，后面我们一步步分解这张电路图。

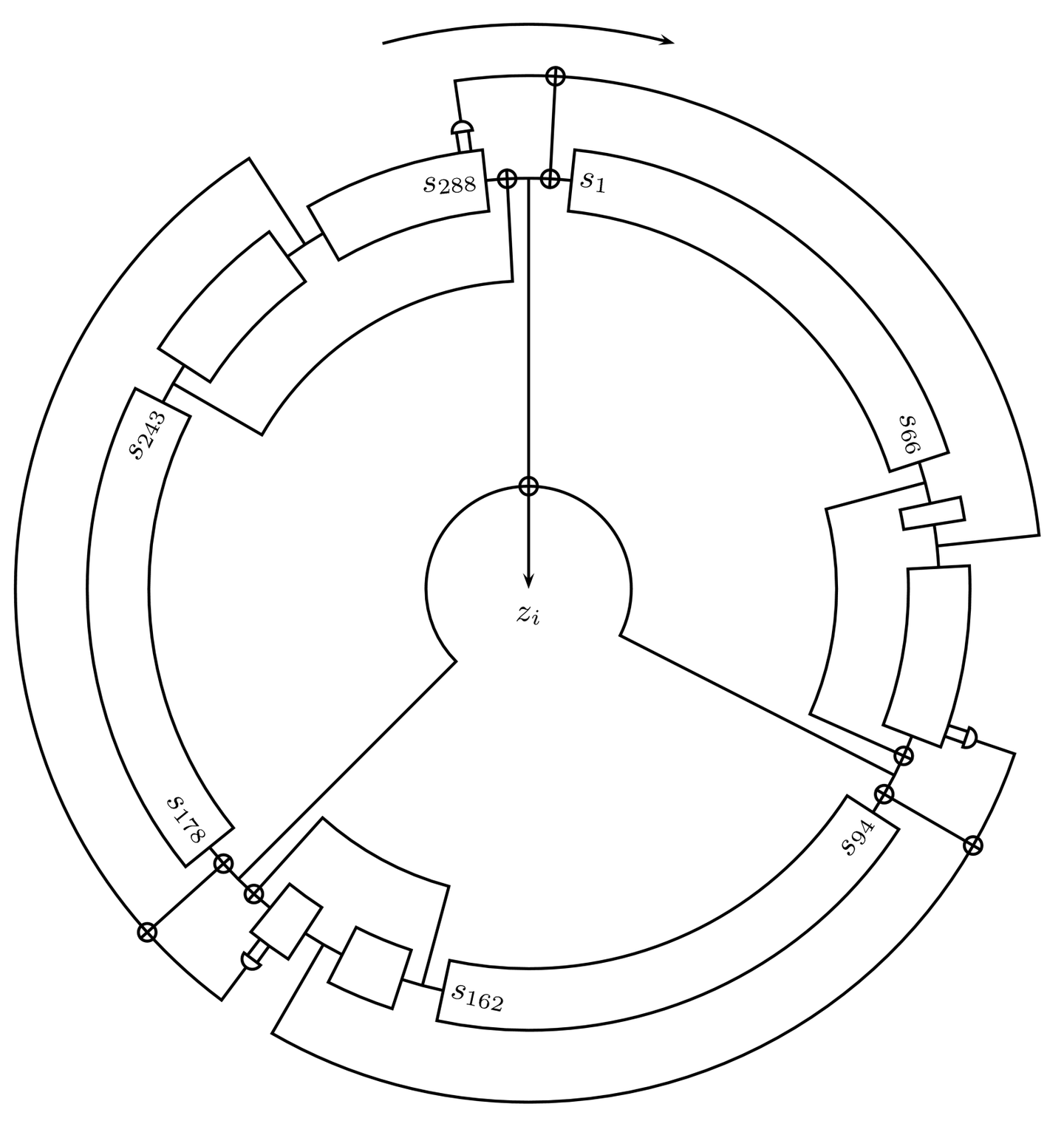
我们划分一下，这个电路其实是由三个 NLFSR (Non-linear Feedback Shift Register) 组成，比如提到的 Trivium 内部状态由 288 个 bit 决定 $S_1...S_{288}$，这 288 个 bit 其实由三个 NLFSR 组成，$S_1...S_{93}，S_{94}...S_{177}，S_{178}...S_{288}$。

下面 1 2 3 圈出来的就是 3 个 NLFSR（红蓝绿），后面会介绍为什么它是 Non-linear Feedback。

我们先解释一下电路的输出，可以看到中间 $Z_i$ 就是三个电路的输出 $T_1, T_2, T_3$（红蓝绿）相加，连到了一个异或门上，中间的电路也就解释了公式 $Z_i=T_1 \oplus T_2 \oplus T_3$ 的由来。

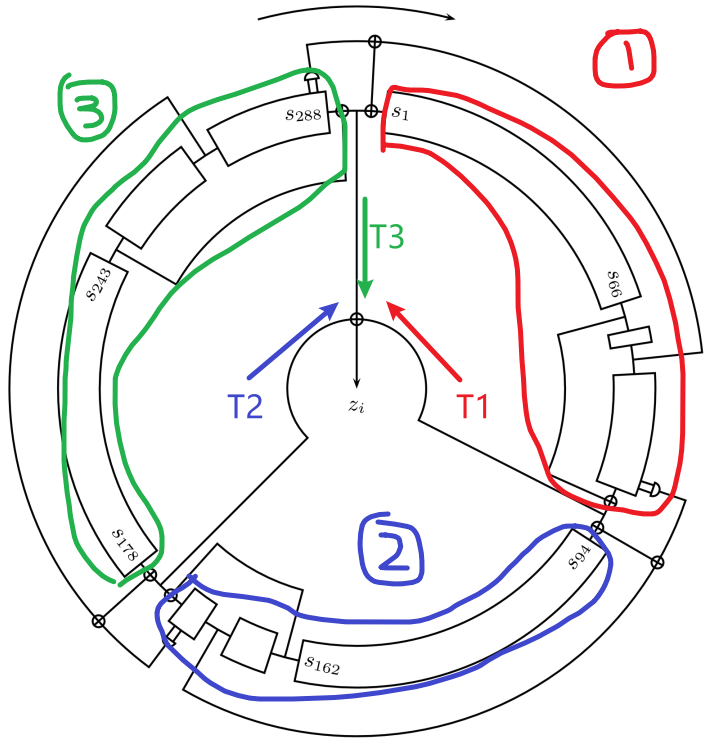
比如我们再解释一下公式 $T_1= S_{66} \oplus S_{93}$，也就是下面图上右下角的 $T_1$ 是怎么计算的，其实就是第一个 NLFSR 的第 66 位，连出来一根导线，和第 93 位一起接到了一个异或门上，它俩相加（异或）的结果再用导线接到了输出 $Z_i$ 。

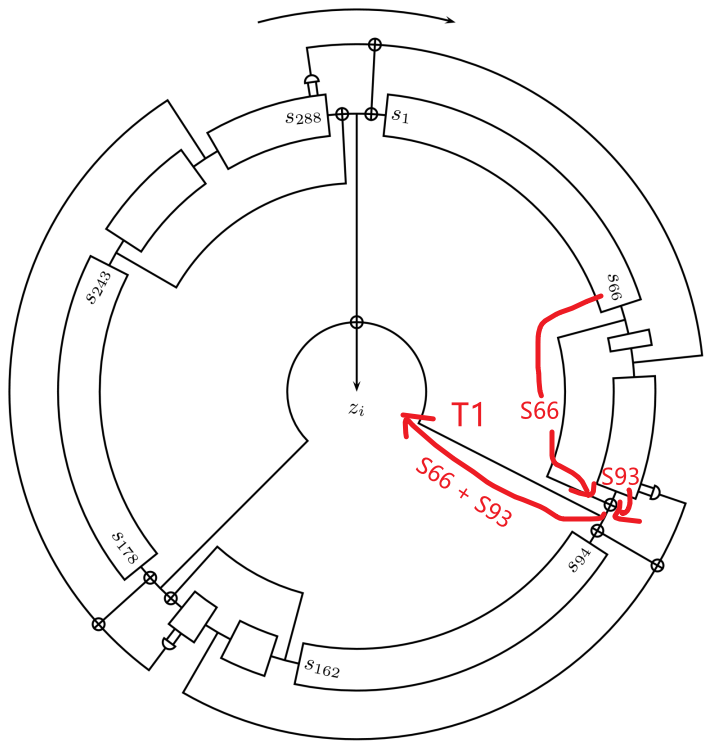
同样，我们也可以用电路解释公式 $T_2=S_{162}\oplus S_{177}$ 和公式 $T_3=S_{243}\oplus S_{288}$。

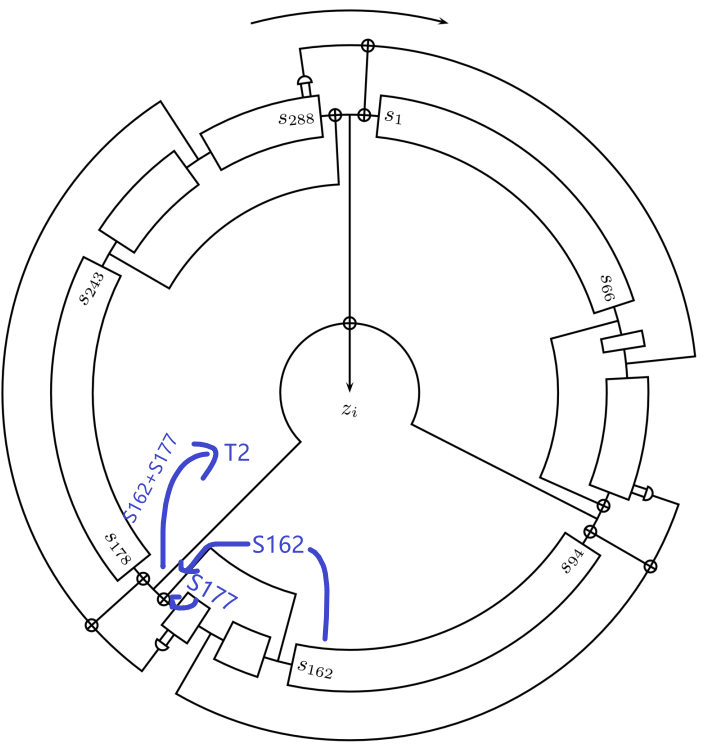
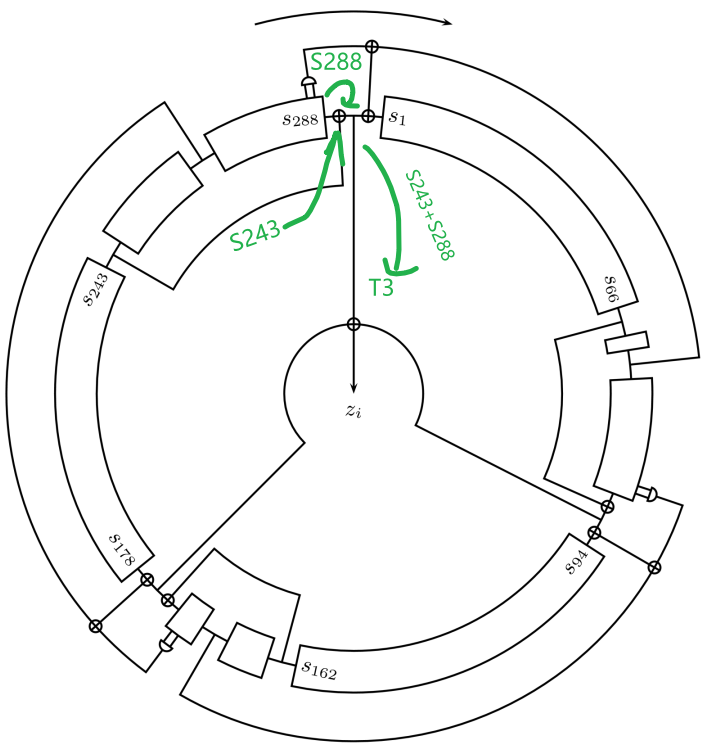
我们继续用电路解释一下公式 $T_1=T_1\oplus S_{91} \wedge S_{92} \oplus S_{171}$，从下面的图上可以看出，这其实就是移位寄存器，把寄存器的最后一位用新的数值替代了。

顺便一提，这里可以看到我们引入了 $\wedge$ 与 (AND) 运算，在二进制里，与 (AND) 运算相当于乘法，于是引入了非线性项，所以前面说这是个 NLFSR (Non-linear Feedback Shift Register) 。

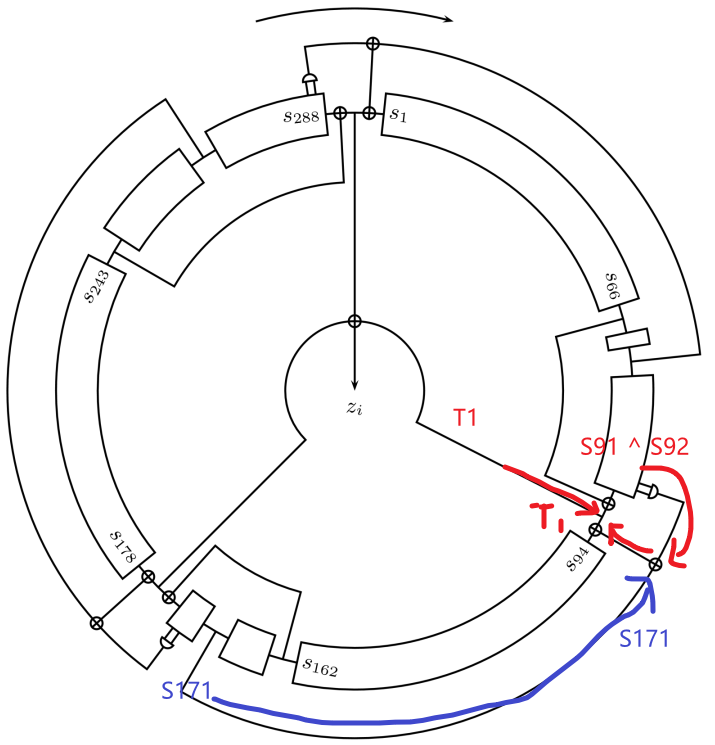
现在，我们再看一遍 Trivium 算法的计算公式，豁然开朗，毕竟可以把它们想象成电路理解了。

或者我们把这个圆形电路平着放看起来更清晰：

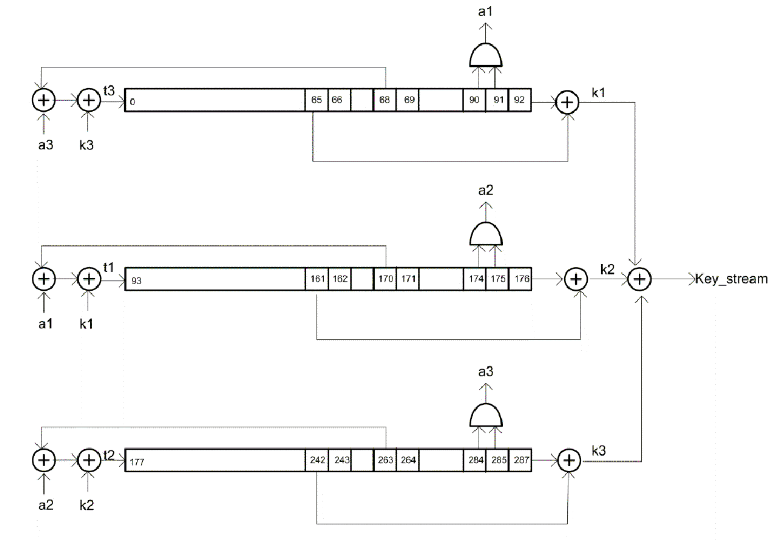
现在我们知道 Trivium 本身的设计其实就是一个由 3 个 NLFSR 组成的数字电路，非常适合在硬件上实现，Tri 英文里也有 3 的意思，而 Trivium 流加密的 Key 和 IV 其实也藏在这个电路里，上面图中 3 个 NLFSR 的初始状态就是由 Key 和 IV 决定的，空余位用 0 或者 1 填充。

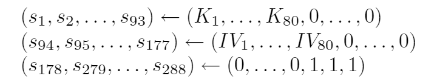
这里顺便解释一下，为什么需要 Key 和 IV。

如果我们没有 Key，每次 Trivium 输出的比特位都是固定好的，一下就破解了。虽然加上 Key 后不同密钥加密的结果不一样，不容易破解了，但是光有 Key 没有 IV，如果两个人凑巧用了相同的密钥，加密了相同的数据。例如网站报头 http 都是一样的，那我就知道他肯定用了和我一样的密码。所以在密钥 Key 的基础上加上随机生成的 IV，就能保证即使大家用了一样的密码，加密出来的结果也是不一样的。

最后一提，Trivium 最多只能加密 2^64 bit 的数据，如果数据量超过这个大小，就需要更换 Key 和 IV。

Trivium 虽然是 Stream Cipher，不过设计灵感其实源自于 Block Cipher。因为学术界对 Block Cipher 的研究更加全面，很多时候可以把 Block Cipher 转换成 Stream Cipher。

硬件实现 (Verilog)

只要理解了前面的算法电路，那么 Verilog 实现就很清楚了。我们只需要定义三个 NLFSR，再把寄存器中间对应的比特位，和输出用导线连起来就可以了。

module cipher_engine(
    /* Standard control signals */
    input   wire            clk_i,      /* System clock */
    input   wire            n_rst_i,    /* Asynchronous active low reset */
    input   wire            ce_i,       /* Chip enable */
    
    /* Data related signals */
    input   wire    [31:0]  ld_dat_i,   /* External data */
    input   wire    [2:0]   ld_reg_a_i, /* Load external value into A */
    input   wire    [2:0]   ld_reg_b_i, /* Load external value into B */
    input   wire            dat_i,      /* Input bit */
    output  wire            dat_o       /* Output bit */
);

//////////////////////////////////////////////////////////////////////////////////
// Signal definitions
//////////////////////////////////////////////////////////////////////////////////
wire    reg_a_out_s;    /* reg_a output */
wire    reg_b_out_s;    /* reg_b output */
wire    reg_c_out_s;    /* reg_c output */
wire    z_a_s;          /* Partial key stream output from reg_a */
wire    z_b_s;          /* Partial key stream output from reg_b */
wire    z_c_s;          /* Partial key stream output from reg_c */
wire    key_stream_s;   /* Key stream bit */

//////////////////////////////////////////////////////////////////////////////////
// Module instantiations
//////////////////////////////////////////////////////////////////////////////////
shift_reg #(
        .REG_SZ(93),
        .FEED_FWD_IDX(65),
        .FEED_BKWD_IDX(68)
    ) 
    reg_a(
        .clk_i(clk_i),
        .n_rst_i(n_rst_i),
        .ce_i(ce_i),
        .ld_i(ld_reg_a_i),
        .ld_dat_i(ld_dat_i),
        .dat_i(reg_c_out_s),
        .dat_o(reg_a_out_s),
        .z_o(z_a_s)
    );
   
shift_reg #(
        .REG_SZ(84),
        .FEED_FWD_IDX(68),
        .FEED_BKWD_IDX(77)
    ) 
    reg_b(
        .clk_i(clk_i),
        .n_rst_i(n_rst_i),
        .ce_i(ce_i),
        .ld_i(ld_reg_b_i),
        .ld_dat_i(ld_dat_i),
        .dat_i(reg_a_out_s),
        .dat_o(reg_b_out_s),
        .z_o(z_b_s)
    );
   
shift_reg #(
        .REG_SZ(111),
        .FEED_FWD_IDX(65),
        .FEED_BKWD_IDX(86)
    ) 
    reg_c(
        .clk_i(clk_i),
        .n_rst_i(n_rst_i),
        .ce_i(ce_i),
        .ld_i(ld_reg_b_i),    /* This is only necessary s.t. the reg will contain 1110000...00 */
        .ld_dat_i(0),
        .dat_i(reg_b_out_s),
        .dat_o(reg_c_out_s),
        .z_o(z_c_s)
    );
   
//////////////////////////////////////////////////////////////////////////////////
// Output calculations
//////////////////////////////////////////////////////////////////////////////////
assign key_stream_s = z_a_s ^ z_b_s ^ z_c_s;
assign dat_o = dat_i ^ key_stream_s;

endmodule

这个实现用的是小端序 (Little Endian)，并且可以使用 iverilog 编译仿真。

$ iverilog -o trivium cipher_engine.v shift_reg.v trivium_top.v trivium_top_tb.v
$ ./trivium

软件实现 (C & Python)

Trivium 本身就是硬件电路，所以使用硬件实现效率更高，当然也可以纯用软件实现那几个公式。

例如下面 Python 实现，初始化好 Key 和 IV，传入初始化 Trivium，就可以得到 Keystream 加密了。

# Key IV are little endian bits
KEY = hex_to_bits("0F62B5085BAE0154A7FA")[::-1]
IV = hex_to_bits("288FF65DC42B92F960C7")[::-1]

# Encoding a string
trivium_encoder = Trivium(KEY, IV)
cipher = trivium_encoder.encrypt("hello")

Keystream 的生成就完全是照搬公式，没有硬件实现看起来那么优美了。

def _gen_keystream(self):
    """this method generates triviums keystream"""

    t_1 = self.state[65] ^ self.state[92]
    t_2 = self.state[161] ^ self.state[176]
    t_3 = self.state[242] ^ self.state[287]

    out = t_1 ^ t_2 ^ t_3

    a_1 = self.state[90] & self.state[91]
    a_2 = self.state[174] & self.state[175]
    a_3 = self.state[285] & self.state[286]

    s_1 = a_1 ^ self.state[170] ^ t_1
    s_2 = a_2 ^ self.state[263] ^ t_2
    s_3 = a_3 ^ self.state[68] ^ t_3

    self.state.rotate(1)

    self.state[0] = s_3
    self.state[93] = s_1
    self.state[177] = s_2

    return out

当然，C 软件实现和 Python 几乎差不多，也是得到 Keystream 后进行异或运算，加密和解密。

// Initialize the trivium cipher
trivium_ctx* ctx = trivium_init(key, iv);

// Write the IV to the output file
for (i = 0; i < 10; i++)
{
    fwrite(&iv[i], 1, 1, outFile);
}

// Encrypt the file
while(fread(&buffer, 1, 1, pFile) != 0)
{
    // XOR the data with keystream
    encbuffer = buffer ^ trivium_gen_keystream(ctx);
    fwrite(&encbuffer, 1, 1, outFile);
}

中间 Keystream 的生成也是不那么优雅地照搬公式。

static uint8_t trivium_rotate(uint8_t *arr, uint8_t arr_size)
{
    uint8_t i;

    uint8_t t1 = trivium_nbit(arr, 66) ^ trivium_nbit(arr, 93);
    uint8_t t2 = trivium_nbit(arr, 162) ^ trivium_nbit(arr, 177);
    uint8_t t3 = trivium_nbit(arr, 243) ^ trivium_nbit(arr, 288);

    uint8_t out = t1 ^ t2 ^ t3;

    uint8_t a1 = trivium_nbit(arr, 91) & trivium_nbit(arr, 92);
    uint8_t a2 = trivium_nbit(arr, 175) & trivium_nbit(arr, 176);
    uint8_t a3 = trivium_nbit(arr, 286) & trivium_nbit(arr, 287);

    uint8_t s1 = a1 ^ trivium_nbit(arr, 171) ^ t1;
    uint8_t s2 = a2 ^ trivium_nbit(arr, 264) ^ t2;
    uint8_t s3 = a3 ^ trivium_nbit(arr, 69) ^ t3;

    /* Begin trivium_rotate */

    for(i = arr_size - 1; i > 0; i--)
    {
        arr[i] = (arr[i - 1] << 7) | (arr[i] >> 1);
    }
    arr[0] = arr[0] >> 1;

    /* End trivium_rotate */

    trivium_change_bit(arr, 1, s3);
    trivium_change_bit(arr, 94, s1);
    trivium_change_bit(arr, 178, s2);

    return out;
}

References

• A stream cipher construction inspired by block cipher design principles.
• On the design of Trivium.
• Trivium hardware implementations for power reduction.
• Trivium specifications.