Quaternion 与三维空间旋转

无论是做游戏开发 (Unity3D / Unreal 5)、无人机，还是无人驾驶，相信很多人都听说过 Quaternion (四元数)。

举个例子，无人机如果用 欧拉角 计算旋转姿态，就会像下面左边那样坠机；而使用 Quaternion 的话受到扰动后依旧能恢复平稳。

Record_2024_11_03_17_02_41_917.mp4 [video-to-gif output image]

再举个例子，下面是 Unity3D 和 Unreal 游戏引擎的 API，只要是关于旋转的 API 都能发现 Quaternion。

# Unity3D
public static Quaternion Slerp(Quaternion a, Quaternion b, float t);

# Unreal
class unreal.Rotator(roll, pitch, yaw).quaternion()

假如你依旧没有听说过 Quaternion，至少听说过欧拉角，例如一架飞机的姿态可以用 roll, pitch, yaw 表示：

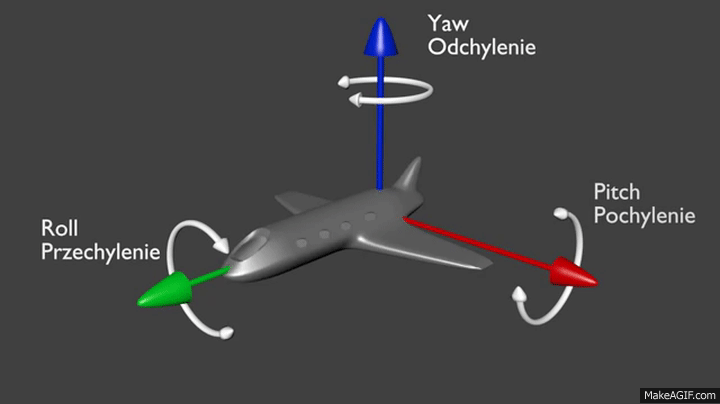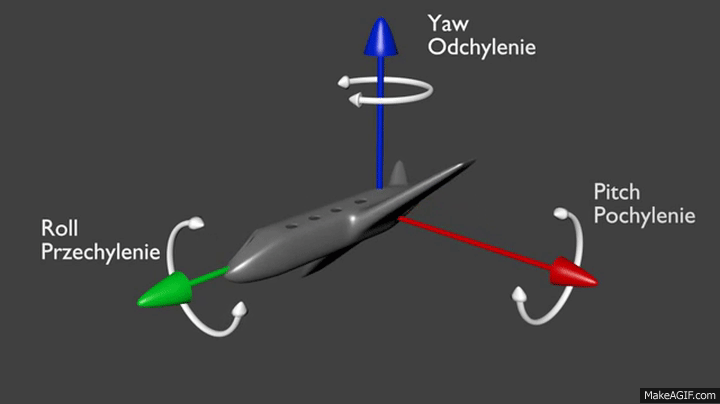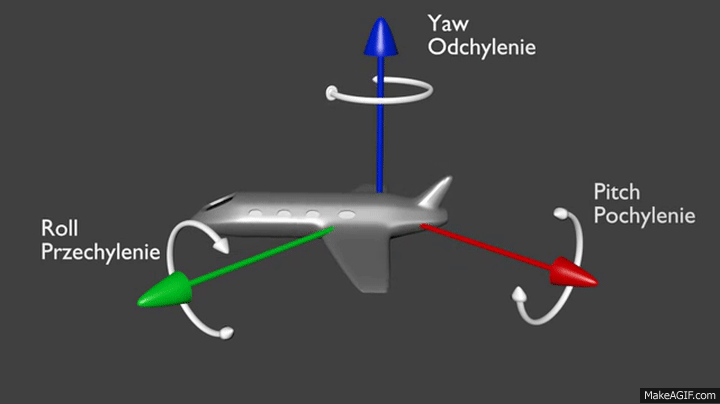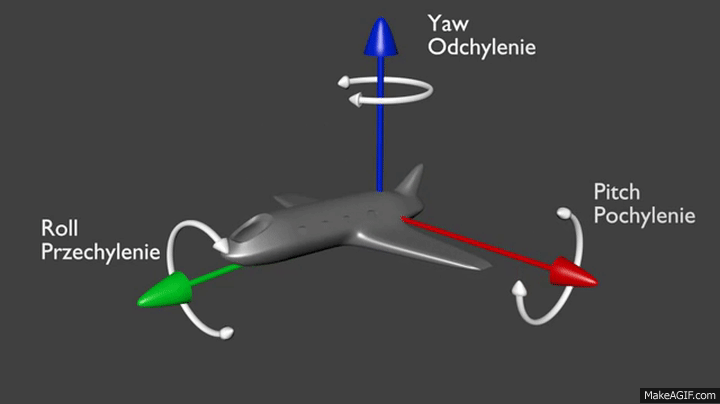
虽然欧拉角的 roll, pitch, yaw 看起来非常直观，但是计算旋转矩阵会非常痛苦。不信的话，我们一起欣赏一下欧拉角最简单的绕 x, y, z 轴旋转矩阵的矩阵。如果是绕任意向量旋转，还会更加复杂。

\begin{aligned} R_{x} (ϕ) R_{y} (θ) R_{z} (ψ) & = [\begin{matrix} \cos (ϕ) & - \sin (ϕ) & 0 \\ \sin (ϕ) & \cos (ϕ) & 0 \\ 0 & 0 & 1 \end{matrix}] [\begin{matrix} \cos (θ) & 0 & \sin (θ) \\ 0 & 1 & 0 \\ - \sin (θ) & 0 & \cos (θ) \end{matrix}] [\begin{matrix} \cos (ψ) & - \sin (ψ) & 0 \\ \sin (ψ) & \cos (ψ) & 0 \\ 0 & 0 & 1 \end{matrix}] \\ = [\begin{matrix} \cos (ψ) \cos (θ) & \cos (ψ) \sin (θ) \sin (ϕ) - \sin (ψ) \cos (ϕ) & - \cos (ψ) \sin (θ) \cos (ϕ) - \sin (ψ) \sin (ϕ) \\ \sin (ψ) \cos (θ) & \sin (ψ) \sin (θ) \sin (ϕ) + \cos (ψ) \cos (ϕ) & - \sin (ψ) \sin (θ) \cos (ϕ) + \cos (ψ) \sin (ϕ) \\ - \sin (θ) & \sin (ϕ) \cos (θ) & \cos (θ) \cos (ϕ) \end{matrix}] \end{aligned}

$\begin{align} R_x(\phi)R_y(\theta)R_z(\psi) &= \begin{bmatrix} \cos(\phi) & -\sin(\phi) & 0 \\ \sin(\phi) & \cos(\phi) & 0 \\ 0 & 0 & 1 \end{bmatrix}\begin{bmatrix} \cos(\theta) & 0 & \sin(\theta) \\ 0 & 1 & 0 \\ -\sin(\theta) & 0 & \cos(\theta) \end{bmatrix}\begin{bmatrix} \cos(\psi) & -\sin(\psi) & 0 \\ \sin(\psi) & \cos(\psi) & 0 \\ 0 & 0 & 1 \end{bmatrix} \\ &= \begin{bmatrix} \cos(\psi) \cos(\theta) & \cos(\psi) \sin(\theta) \sin(\phi) - \sin(\psi) \cos(\phi) & -\cos(\psi) \sin(\theta) \cos(\phi) - \sin(\psi) \sin(\phi) \\ \sin(\psi) \cos(\theta) & \sin(\psi) \sin(\theta) \sin(\phi) + \cos(\psi) \cos(\phi) & -\sin(\psi) \sin(\theta) \cos(\phi) + \cos(\psi) \sin(\phi) \\ -\sin(\theta) & \sin(\phi) \cos(\theta) & \cos(\theta) \cos(\phi) \end{bmatrix} \end{align}$

另一方面，使用欧拉角会碰到著名的 Gimbal Lock 问题，也就是下图这样：如果使用旋转矩阵，每当飞机的姿态与某个轴重合的时候，就会突然绕另一个轴旋转，如果无人机出现这个问题当然就是坠机了。

Record_2024_11_04_19_11_16_497.mp4 [optimize output image]

Quaternion 则可以解决 Gimbal Lock，同时计算也会更简单。
Quaternion 有四个维度，分别用虚轴 $i, j ,k$ 表示三个虚轴。
Quaternion (四元数): $q=a+b \textbf{i} + c\textbf{j} + d \textbf{k}$

完蛋，一看到虚数，很多人可能就头大，不禁回想起本科一元分析、多元分析、复分析的恐惧。于是决定写这篇文章，用动画和图片的方式，直白地演示 Quaternion 怎么用虚数表示三维空间的姿态。

2维虚数: i

首先，我们从最简单的 2维平面开始，提到虚数很多人第一印象可能就是下面的公式。

i^{2} = - 1

$i^2=-1$
都说

x^{2}

$x^2$ 平方大于等于 0，怎么还会有

i^{2} = - 1

$i^2=-1$ 啊？其实我们只需要换个角度，就豁然开朗了。

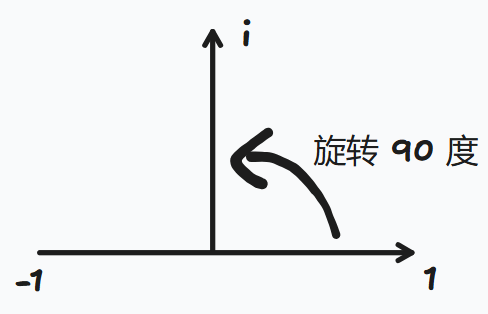
我们把 $i$ 想象成旋转 90°，比如从 1 开始，逆时针旋转 90 °，就成了 $i$ ；

1 * i = i

$1 * i = i$

我们把 $i$ 继续旋转 90°，就从 $i$ 旋转到了 -1。

i * i = - 1

$i * i = -1$

这样是不是理解，为什么 $i^2=-1$ 了，每次和 $i$ 相乘就是旋转 90°。其实就是先从 1 旋转 90°到 $i$ 轴，再旋转一次就成了 -1 负轴。

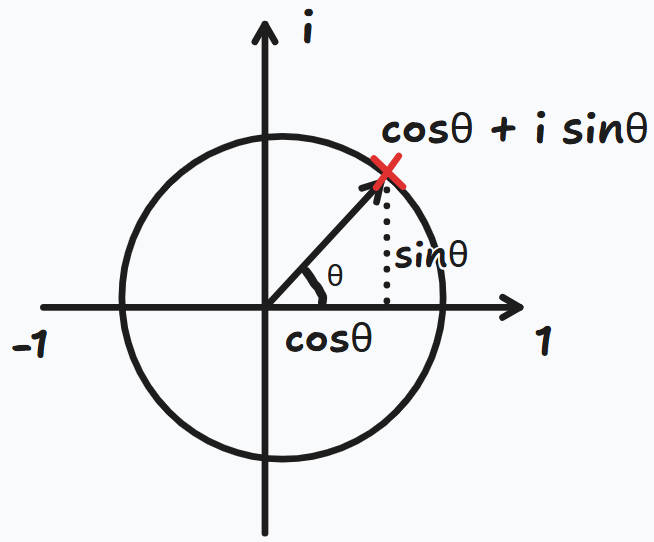
假设我们旋转任意角度 θ，那么单位圆上的任一点就都能用复数表示了：

z = c o s θ + i s i n θ

$z = cos\theta + i sin\theta$
这样用旋转来理解虚数

i

$i$ ，相信容易了不少，上面的

z

$z$ 我们就可以理解成逆时针旋转

θ

$\theta$ 。

那么如果我们先旋转 $\theta_1$ ，再旋转 $\theta_2$ ，会怎么样呢？相信大家都知道最终角度是 $\theta_1+\theta_2$ ，但是我们需要证明一下。

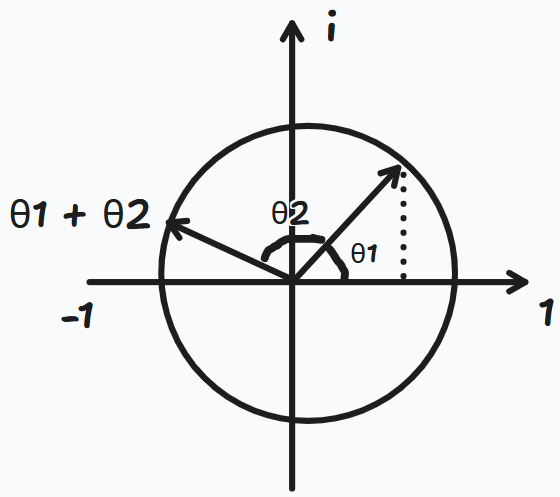
如果我们把复数理解为旋转，两次旋转 $\theta_1 + \theta_2$ 则是把两个复数 $z_1$ 和 $z_2$ 相乘：

第一次旋转 $\theta_1$ ： $z_1=cos\theta_1+isin\theta_1$
第二次旋转 $\theta_2$ ： $z_2=cos\theta_2+isin\theta_2$

\begin{aligned} z_{1} * z_{2} & = (c o s θ_{1} + i s i n θ_{1}) (c o s θ_{2} + i s i n θ_{2}) \\ = (c o s θ_{1} c o s θ_{2} - s i n θ_{1} s i n θ_{2}) + i (c o s θ_{1} s i n θ_{2} + s i n θ_{1} c o s θ_{2}) \\ = c o s (θ_{1} + θ_{2}) + i s i n (θ_{1} + θ_{2}) \end{aligned}

$\begin{align} z_1*z_2 &=(cos\theta_1+isin\theta_1)(cos\theta_2+isin\theta_2)\\ &= (cos\theta_1cos\theta_2-sin\theta_1sin\theta_2) + i(cos\theta_1sin\theta_2+sin\theta_1cos\theta_2)\\ &= cos(\theta_1+\theta_2)+ isin(\theta_1+\theta_2) \end{align}$

于是，两个复数相乘 $z_1z_2$ ，其实就是旋转角度相加 $\theta_1 + \theta_2$ 。一提到乘法等于加法，你可能立马想起来指数 $e$ 不就是这样吗：

e^{a} * e^{b} = e^{a + b}

$e^{a} * e^{b}=e^{a+b}$
这就是为什么也有人用指数

e^{i θ}

$e^{i\theta}$ 表示复数旋转：

e^{i θ} = c o s θ + i s i n θ

$e^{i\theta}=cos\theta + i sin\theta$
比如我们先旋转

e^{i θ_{1}}

$e^{i\theta_1}$ ，再旋转

e^{i θ_{2}}

$e^{i\theta_2}$ ，那么最后的位置就是

e^{i (θ_{1} + θ_{2})}

$e^{i(\theta_1+\theta_2)}$ 。

e^{i θ_{1}} * e^{i θ_{2}} = e^{i （ θ_{1} + θ_{2})} = c o s (θ_{1} + θ_{2}) + i s i n (θ_{1} + θ_{2})

$e^{i\theta_1} * e^{i\theta_2}=e^{i（\theta_1+\theta_2)}=cos(\theta_1+\theta_2) + i sin(\theta_1+\theta_2)$

到这里位置，相信你不再觉得复数 $i$ 很离谱，很头大了，其实它就是代表二维平面的旋转。

\begin{aligned} z = e^{i θ} = c o s θ + i s i n θ \end{aligned}

$\begin{align} z = e^{i\theta} = cos\theta+isin\theta \end{align}$

Record_2024_11_04_19_27_14_705.mp4 [optimize output image]

四维 Quaternion: i, j, k

前面提到 Quaternion 是四维的，可能一下从二维跳到四维太突兀了，我们先看看三维的情况：

q = c o s θ + s i n θ (a i + b j)

$q = cos\theta + sin\theta(a\textbf{i} + b\textbf{j})$
这里说是三维，其实不过是多了个虚轴

j

$j$ 罢了，如果我们俯视这个三维的球体，会发现改变

i, j

$i, j$ 的参数，其实就是在旋转一个二维的单位向量

a i + b j

$ai + bj$ ，其中

a^{2} + b^{2} = 1

$\ a^2+b^2=1$ 表示单位圆上的点。

Record_2024_11_04_19_34_46_65.mp4 [video-to-gif output image]

那么我们固定这个二维的向量 $ai + bj$ ，再改变 $\theta$ 是什么效果呢？注意看下面动画圈出来的红色向量，其实改变的就是与这个二维向量的夹角 $\theta$ 。如果我们切换到与 $ai+bj$ 垂直的正视图，又看到一个单位圆的旋转了。

q = c o s θ + s i n θ (a i + b j)

$q = cos\theta + sin\theta(a\textbf{i} + b\textbf{j})$

Record_2024_11_04_19_58_29_2.mp4 [optimize output image]

相信现在你已经理解了 2维、3维的空间旋转，但是别忘了，我们还可以自转呢。于是我们再增加一个维度就有了 Quaternion，其实就是先找到一个三维向量 $ai+bj+ck$ ，再绕着这个向量旋转 $\theta$ ：

q = c o s θ + s i n θ (a i + b j + c k)

$q = cos\theta + sin\theta (a\textbf{i} + b\textbf{j} + c\textbf{k})$

还是注意红色箭头圈出来的向量，其实我们改变 ( $i, j, k$ ) 就是改变这个三维向量在空间里的位置，最后不出意外的话，剩下的 $\theta$ 就是与这个三维向量的夹角了。

Record_2024_11_04_20_08_03_356.mp4 [optimize output image]

当然，我们还是需要改变 $\theta$ 看 Quaternion 是如何绕三维向量 $ai+bj+ck$ 旋转的。

Record_2024_11_04_20_13_45_604.mp4 [optimize output image]

可以看到，果然是绕三维向量 $ai+bj+ck$ 自转。相信你现在已经理解 Quaternion 是怎么表示三维空间姿态的了，以及为什么我们需要四个维度。

q = c o s θ + s i n θ (a i + b j + c k)

$q = cos\theta + sin\theta (a\textbf{i} + b\textbf{j} + c\textbf{k})$
当然，你也可以自己去这个网站上体验一下 Quaternion 的乐趣。

Visualize Quaternion: https://eater.net/quaternions/video/intro

最后，我们看看 Quaternion 的旋转公式，一个向量 $p$ 绕任意三维向量 $q$ 旋转 $\theta$ 后的向量 $p^{'}$ ，公式相比欧拉角的旋转矩阵要简单多了，而且也不会有文章开头 Gimbal Lock 的问题，因为 Quaternion 维度更高有四维：

p^{^{'}} = q p \bar{q}

$p^{'} = qp\bar{q}$

q = c o s \frac{θ}{2} + u s i n \frac{θ}{2}

$q = cos\frac{\theta}{2} + usin\frac{\theta}{2}$

u = u_{x} i + u_{y} j + u_{z} k

$u = u_xi+u_yj+u_zk$

如果你想问，为什么是 $cos \frac{\theta}{2} + usin\frac{\theta}{2}$ ，而不是 $\theta$ 可以在这里找到证明过程：Euler-Rodrigues-Hamilton。

https://www.math.stonybrook.edu/~oleg/courses/mat150-spr16/lecture-5.pdf

总结

现在你应当理解什么是虚数，为什么 $i^2=-1$ 了，以及我们为什么需要四维的 Quaternion 来表示三维空间的旋转了。Quaternion 不仅旋转公式简单，还不会有 Gimbal Lock 的问题。

另外，也有人用下面的公式表示 Quaternion，只要你还记得单位球的旋转动画，应该能猜到： $w^2 + a^2 + b^2 + c^2 = 1$ 。

q = w + a i + b j + c k

$q = w + a\textbf{i} + b\textbf{j} + c\textbf{k}$
最后顺便一提，Quaternion 的乘法遵循

i i = j j = k k = - 1, i j = - j i = k, i j k = - 1

$ii=jj=kk=-1, ij=-ji=k, ijk=-1$ ，如果我们把两个

w = 0

$w=0$ 的 Quaternion 相乘会发现很有意思的事情：

q_{1} = a_{1} i + b_{1} j + c_{1} k q_{2} = a_{2} i + b_{2} j + c_{2} k

$q_1 = a_1\textbf{i} + b_1\textbf{j} + c_1\textbf{k}\\ q_2 = a_2\textbf{i} + b_2\textbf{j} + c_2\textbf{k}$

\begin{aligned} q_{1} q_{2} & = (a_{1} i + b_{1} j + c_{1} k) (a_{2} i + b_{2} j + c_{2} k) \\ = - (a_{1} a_{2} + b_{1} b_{2} + c_{1} c_{2}) + (b_{1} c_{2} - b_{2} c_{1}) i - (a_{1} c_{2} - a_{2} c_{1}) j + (a_{1} b_{2} - a_{2} b_{1}) k \\ = - q_{1} \cdot q_{2} + q_{1} \times q_{2} \end{aligned}

$\begin{align} q_1q_2 &= (a_1\textbf{i} + b_1\textbf{j} + c_1\textbf{k})(a_2\textbf{i} + b_2\textbf{j} + c_2\textbf{k}) \\ &= -(a_1a_2+b_1b_2+c_1c_2) + (b_1c_2-b_2c_1)i-(a_1c_2-a_2c_1)j+(a_1b_2-a_2b_1)k \\ &= -q_1\cdot q_2 + q_1 \times q_2 \end{align}$

最后结果的实部 $-q_1\cdot q_2$ ，不就是负的向量内积吗？
最后结果的虚部 $q_1 \times q_2$ ，则是向量的外积。

现在你可能理解为什么向量的内积是一个数值 (实部)，向量的外积是一个向量 (虚部 $i, j, k$ ) 了，其实内积和外积，是源自于更高维度的 Quaternion 乘法。

Quaternion 与 三维空间旋转

2维虚数: i

四维 Quaternion: i, j, k

总结

Quaternion 与三维空间旋转