Magnetometer 磁力计校正

相信很多人都用过指南针，但是磁力计就不一定直接接触过，可能会问磁力计为什么要校正呢？毕竟指南针不是一直指向南极吗？实际上并不是。

以前学过电场产生磁场，可能知道地球内部有一圈液态金属，充满电荷的液态金属随着地球的自转而旋转，就会形成电磁场。可能很多人根据右手定则，印象中地球的磁场是长这样的，类似标准的条形磁铁。

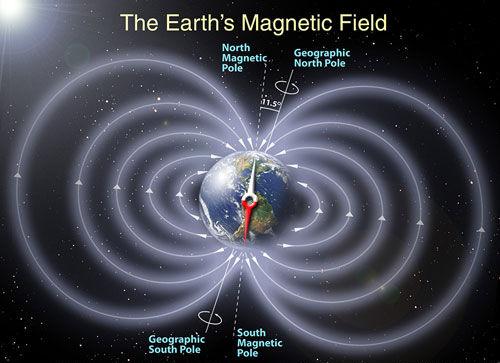
然而很不幸的是，一方面地球内部液态金属的流动非常复杂，并不是简单的右手定则线圈能描述的；另一方面，太阳也会不断向地球辐射带电粒子，让地球的磁场产生扭曲，实际上地球的磁场长这样：

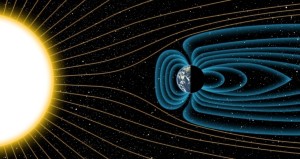
所以地球的磁极并不会穿过南北极，以至于跟着指南针一路走并不会抵达南极。

更糟糕的是，由于地核温度的变化，磁场还会随着时间和位置变化，下面动画展示了最近四百年来地球磁场的变化可以看到地球的磁极一年四季不停地改变位置。

Record_2024_11_03_00_28_34_987.mp4 [optimize output image]

因此，当我们使用磁力计的时候，它指向的是磁场的极点，而不是地球旋转轴的南北极。如果想要去地理位置的南北极，我们就需要校正：这种地理南北极和磁场南北极的偏差，称为 Magnetic Declination。

当我们使用磁力计的时候，一共需要校正三种磁场偏差：

Magnetic Declination
Hard-Iron Calibration
Soft-Iron Calibration

Magnetic Declination

第一种偏差是最容易校正的，前面已经介绍过了，地磁的南北极和地球自转轴的南北极有一个偏差。这种偏差在不同时间、地球的不同位置都不一样，只要我们根据自己的位置去查表就知道偏差是多少了。

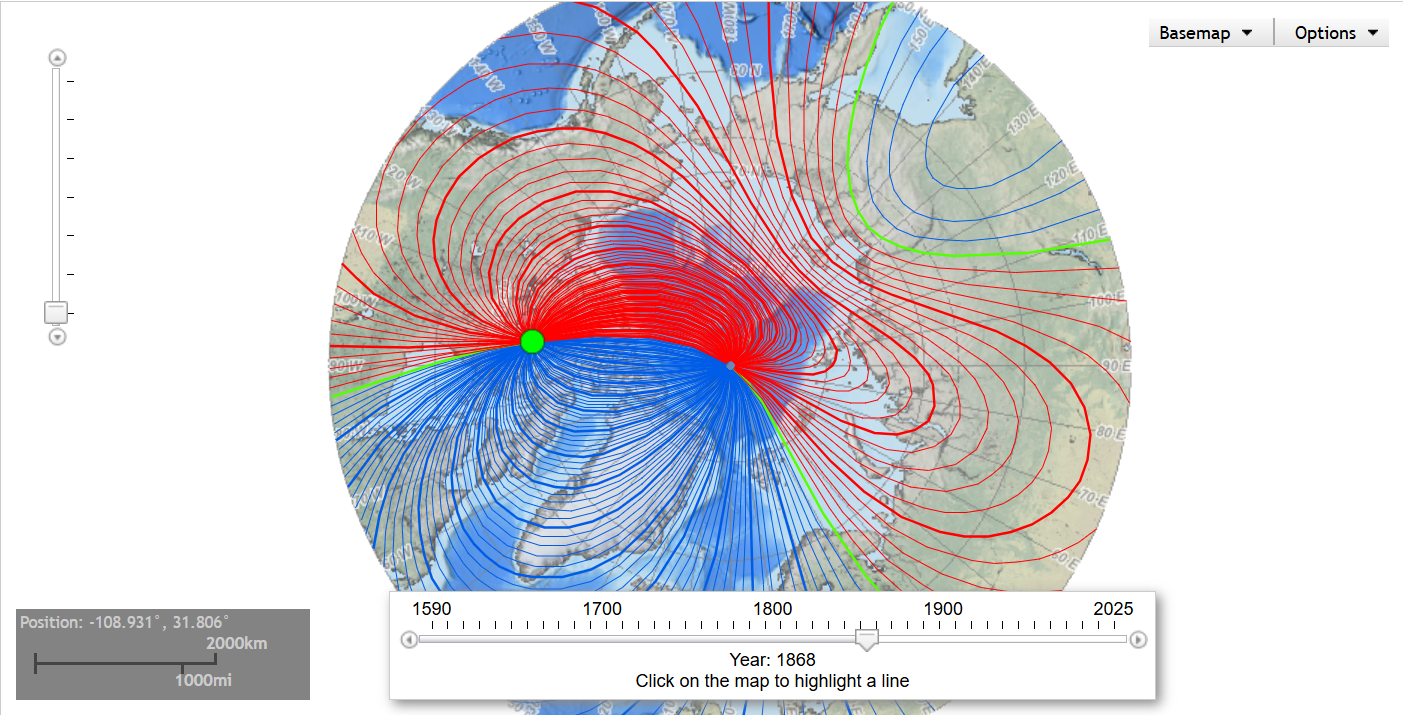
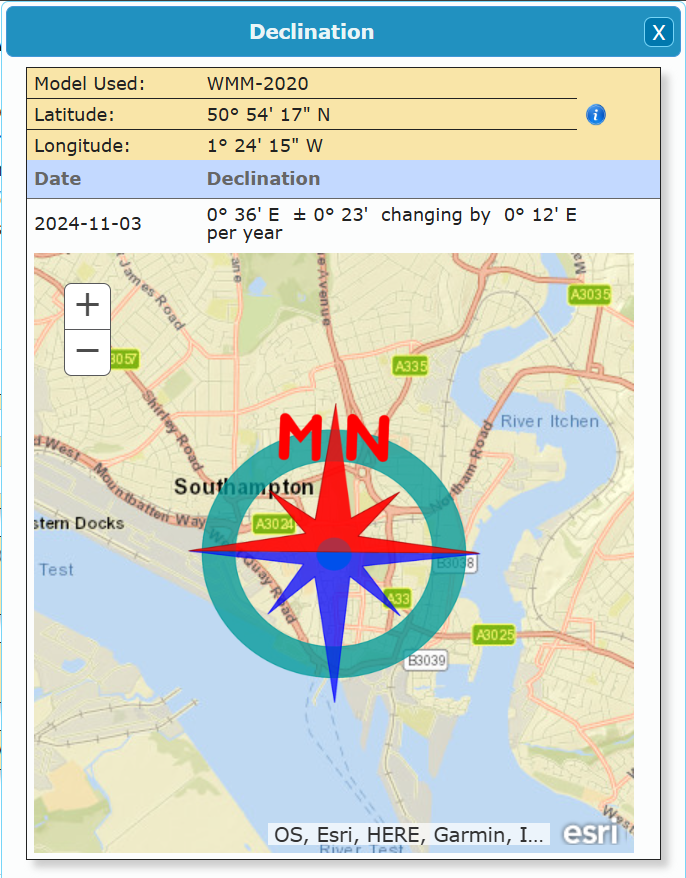
比如在下面这个网站上，可以输入自己的城市位置，然后网站就会计算出 Declination 的偏差值，比如我的是向东边偏差0度36分，每年还会改变0度12分。

https://www.ngdc.noaa.gov/geomag/calculators/magcalc.shtml

顺便一提，偏向西方 (W) 的 Declination 是负值，偏向东方 (E) 的是正值，一行代码就能校正了。

declination = 36' / 60' = 0.6 degree
heading = heading - declination

Hard-Iron Calibration

除了地球自己本身的问题，我们在使用磁力计的时候，可能还会碰到电路板边上有个 永磁铁 造成传感器测量误差，比如机器人的电机是带磁性的，电路板上如果有个喇叭也是带磁的，这种偏差称之为 Hard-Iron。

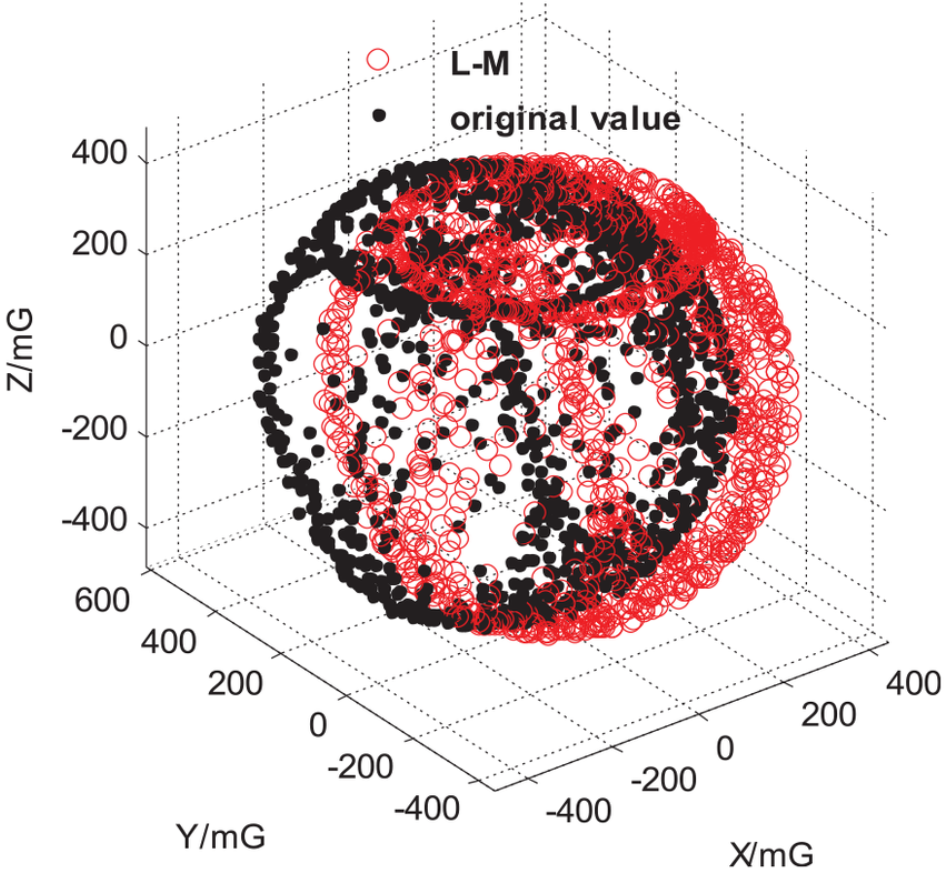
如果没有永磁体干扰，磁力计应该是各向同性的 (Isotropic Sensitivity)，因为地球在同一个点的磁场强度大小基本不会变化，只是方向在不停改变。类似一个固定大小的向量，在三维空间中不停地旋转，理想情况下应当是画出一个球，球的中心在 (0，0) 的位置。

但是如果有永磁体的干扰，这个球的中心可能会发生偏移，所以我们需要先校正把中心点移动到 (0, 0)，这个实现起来也非常简单，就是减去 x, y 方向的偏移值就可以了。

mag_x = mag_x - x_offset
mag_y = mag_y - y_offset
mag_Z = mag_z - z_offset

后面会介绍，怎么用软件 MotionCal 得到 x_offset，y_offset，z_offset。

Soft-Iron Calibration

除了永磁铁会改变磁场强度，我们实际用磁力计的时候，边上可能还有一些磁性材料，它们会让磁场发生弯曲，导致各个方向测得的磁场强度并不一样，把标准的圆变成了椭圆。

所以简单来讲，我们校正磁力计的目的，就是让磁力计的测量再次变成各向同性，中心点在 (0, 0) 的球，而不是偏移到其他地方的椭球。

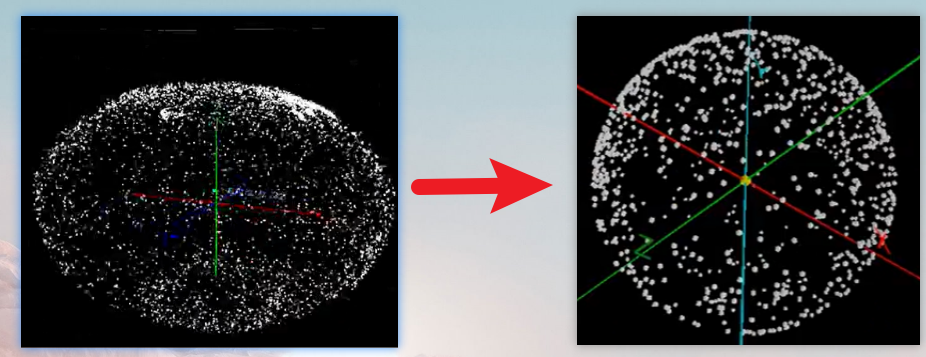
由于 x, y, z 方向的磁场可能被拉伸成椭球，我们需要乘以一个系数按比例把它恢复成球。

如果用 $m_c$ 表示校正后的磁场向量， $[m_x, m_y, m_z]$ 分别是校正前各个方向的磁场强度。如果不存在 Soft-Iron 干扰，这个校正矩阵就是一个对角矩阵，只有对角线上的元素是 1。

m_{c} = [\begin{matrix} 1 & 0 & 0 \\ 0 & 1 & 0 \\ 0 & 0 & 1 \end{matrix}] * [\begin{matrix} m_{x} \\ m_{y} \\ m_{z} \end{matrix}]

$m_{c} = \begin{bmatrix} 1 & 0 & 0 \\ 0 & 1 & 0 \\ 0 & 0 & 1 \end{bmatrix} * \begin{bmatrix} m_x \\ m_y \\ m_z \end{bmatrix}$

但是为了校正椭圆，对角线的系数需要乘以一个比例，可能还需要和其他方向的磁场线性组合，得到最后的校正矩阵，比如我用 MotionCal 软件得到的校正系数：

m_{c} = [\begin{matrix} 0.965 & 0.010 & 0.009 \\ 0.010 & 0.999 & - 0.021 \\ 0.009 & - 0.021 & 1.038 \end{matrix}] * [\begin{matrix} m_{x} \\ m_{y} \\ m_{z} \end{matrix}]

$m_{c} = \begin{bmatrix} 0.965 & 0.010 & 0.009 \\ 0.010 & 0.999 & -0.021 \\ 0.009 & -0.021 & 1.038 \end{bmatrix} * \begin{bmatrix} m_x \\ m_y \\ m_z \end{bmatrix}$

如果再考虑上前面提到的 Hard-Iron 校正，就会得到这样的校正公式 (系数只是演示)：

m_{c} = [\begin{matrix} 0.965 & 0.010 & 0.009 \\ 0.010 & 0.999 & - 0.021 \\ 0.009 & - 0.021 & 1.038 \end{matrix}] * [\begin{matrix} m_{x} + 144 \\ m_{y} - 81 \\ m_{z} + 241 \end{matrix}]

$m_{c} = \begin{bmatrix} 0.965 & 0.010 & 0.009 \\ 0.010 & 0.999 & -0.021 \\ 0.009 & -0.021 & 1.038 \end{bmatrix} * \begin{bmatrix} m_x + 144\\ m_y - 81\\ m_z + 241 \end{bmatrix}$
所以我们校正最重要的就是得到 3x1 的 Hard-Iron 校正系数，和 3x3 的 Soft-Iron 校正矩阵，最终代码其实很简单：

// Hard-Iron Parameters
const int hard_iron[3] = {-144, 81, -241};

// Soft-Iron Parameters
const float soft_iron[3][3] = {
    {0.965, 0.010, 0.009}, 
	{0.010, 0.999, -0.021}, 
	{0.009, -0.021, 1.038}
};

// Hard-Iron Calibration
int hi_cal[3];
hi_cal[0] = mx - hard_iron[0];
hi_cal[1] = my - hard_iron[1];
hi_cal[2] = mz - hard_iron[2];

// Soft-Iron Calibration
float mag_data[3];
for (int i = 0; i < 3; i++) {
  mag_data[i] = (soft_iron[i][0] * hi_cal[0]) +
                (soft_iron[i][1] * hi_cal[1]) +
                (soft_iron[i][2] * hi_cal[2]);
}

到这里，我们校正磁力计的思路就很清楚了：

首先需要去网站上查询自己当地位置的 Magnetic Declination 是多少，再用 MotionCal 或者其他软件得到 Hard-Iron 和 Soft-Iron 的校正系数，最后就是加减法和矩阵乘法了。

MotionCal 软件

那么，怎么使用 MotionCal 软件呢？

软件下载：https://www.pjrc.com/store/prop_shield.html

第一步，我们需要把磁力计连接到 MCU 在串口打印传感器的原始数据，这里不管是使用 Arduino，RT-Thread, Zephyr, Rust Embassy, RIOT 都不太重要，只要能按照下面的格式串口打印数据就能对接 MotionCal 了：

Raw: gx, gy, gz, ax, ay, az, mx, my, mz

这里 gx, gy, gz 分别是陀螺仪的数据，ax, ay, az 是加速度计的数据，mx, my, mz 则是磁力计的数据。当然，校正磁力计我们只需要打印磁力计的数据就足够了，所以我打印出来的数据长这样，陀螺仪和加速度计设置为 0。

Raw: 0, 0, 0, 0, 0, 0, -416, -314, 672

这里注意磁力计数据是3位整数，所以可能需要单位换算，比如原始数据 x1000。

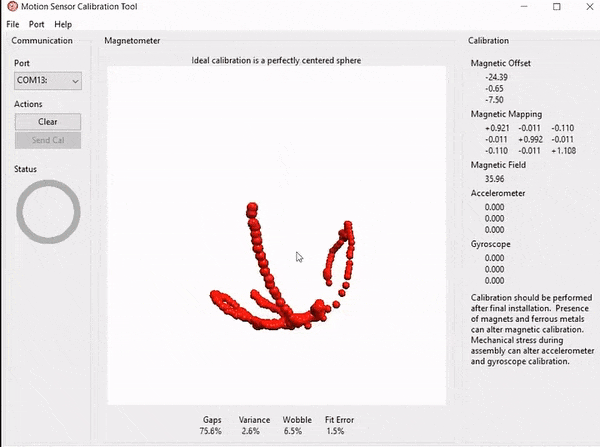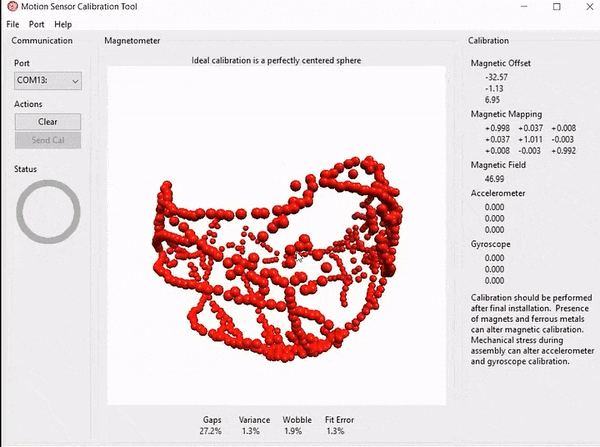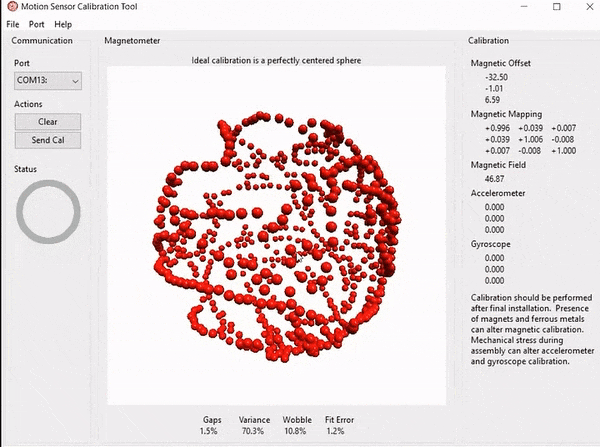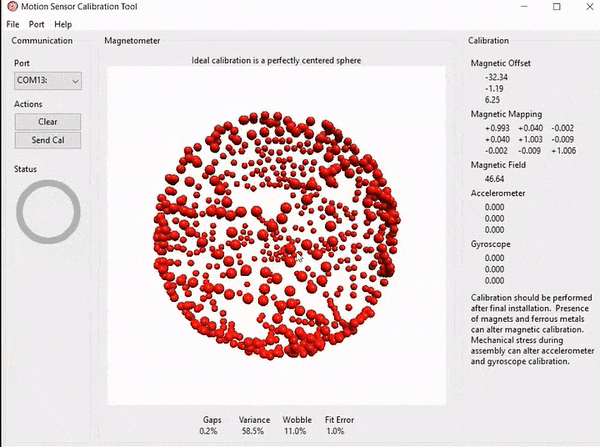
第二步，我们把开发板连接到电脑，MotionCal 连上串口后，接下来就是体力活了，不停地摇晃、倾斜磁力计的角度，尽量画出一个球测出不同方向的磁场强度，软件右边会实时更新校正的矩阵，感觉测量点差不多了我们就可以断开连接，保存矩阵参数。

Image Record_2024_11_03_02_30_46_380.mp4

总结

现在应该理解为什么要校正磁力计，以及校正磁力计需要的三个参数了。

Magnetic Declination
Hard-Iron Calibration
Soft-Iron Calibration

然而这里我还没有介绍另一个很重要的校正：

Tilt Calibration

这里校正完后，如果把磁力计水平放在桌面上，应当会很准确了，然而不幸的是飞控或者机械臂上的磁力计并不一定水平，所以我们还需要根据传感器的倾斜角度，校正 x, y, z 各个方向的磁场分量。

至于传感器的角度估计，当然可以用我之前文章介绍的互补滤波器来估计了，再结合磁力计的方向，我们就能精准得到开发板的 roll, pitch, yaw 姿态了，不过后面我还会介绍更新的 Kalman Filter，Mahony Filter 和 Madgwick Filter。