g-h 滤波器与 PID 控制 (Filter & Control)

之前的一篇文章介绍了 互补滤波器 (Complementary Filter)，并演示了如何从 IMU 原始数据，用互补滤波器得到更准确的加速度和旋转角速度 (核心算法的代码就 7 行)。

在理解了最简单的互补滤波器后，就可以进一步了解稍稍高级一点的 $g-h$ 滤波器（也有人称为 $\alpha-\beta$ 滤波器）。

$\alpha-\beta-\gamma$ 滤波器和 P I D 控制高度相似。

当然，最受欢迎的滤波器当属阿波罗 (Apollo) 登月计划闻名的 卡尔曼滤波器 (Kalman Filter)，但是要理解 Kalman Filter 需要一些理论背景，我会尝试从互补滤波器， $g-h$ Filter，再到 Bayesian Filter，循序渐进到 Kalman Filter 。

简介滤波器
互补滤波器 (Complementary Filter)
$g-h$ 滤波器
贝叶斯滤波器 (Bayesian Filter)
卡尔曼滤波器 (Kalman Filter)

简介滤波器 (Filter)

想起来还没介绍什么是滤波器 (Filter)？

每当提到滤波器，可能很多人脑海里就会有这样一张图：一条皱皱巴巴的曲线，在滤波后变得光滑。

虽然这个例子很形象地告诉我们：各种传感器信号都是有噪声的，滤波器就是为了过滤掉这个噪声。但是这个例子忽略了非常重要的两个概念：预测 (Prediction) 和测量 (Measurement)，这是一个动态的过程。这两个概念可以说贯穿了经典控制理论以及 强化学习。

相比之下，我更喜欢另一个经典例子（不过我忘了这个例子的出处）。

假设你面前有两扇门 A B，一扇门是安全出口，而另一扇门的背后有一只老虎，你不得不选择一扇门离开。

然而很不幸，你提前没有任何信息，无法预测老虎在哪一扇门的背后，于是只能说每一扇门后面都有 50% 的概率是只老虎。(A: 50%，B：50%)

然而幸运的是，你有一双耳朵，可以偷偷听一听门背后的声音，并且你听到 A 出口后面传来了一声虎啸，这个时候你感觉 A 出口很危险。

然而不幸的是，两扇门太近了，耳朵也可能会听错，假如有 80% 概率听对，20% 的概率听错。在经过耳朵测量 (Measurement) 后，你更新了自己的估计 (Prediction)，两扇门后有老虎的概率分别是 A: 80%，B: 20%。

生命只有一次，以防万一，你又偷听了一次，这次又听到 A 出口后传来吼叫声。

由于只有一个门后有老虎：假设老虎在A后面，两次听对的概率 0.8 * 0.8 = 0.64；假设老虎在B后面，两次听错的概率 0.2*0.2 = 0.04。

这里我们认为两扇门不互通，老虎不能随意移动，所以只有上面两种情况。不存在第一次听对，第二次听错（老虎一开始在 A，第二次跑去了 B）

这个时候你更新了自己的估计，两只门后有老虎的概率分别是：

A：0.64 / (0.64 + 0.04) = 0.94
B：0.04 / (0.64 + 0.04) = 0.06

两次观测后，这下你有 94% 的概率相信老虎在 A 后面了，于是大胆地从 B 出口离开了。

这个例子告诉我们观测 (measurement) 的重要性，每一次偷听门后的声音，我们就对老虎的位置有了一个新的估计 (Prediction)。滤波其实就是这样一个动态的过程：在反复的观测中，不断更新自己的估计。

但是现实世界的传感器都是不完美，有噪声的。比如你非常耳背，只有 60% 的概率能听对，有 40% 的概率会听错，这个时候如果你两次听到 A 门后传来了声音，你的估计是：

A：0.36 / (0.36 + 0.16) = 0.69
B：0.16 / (0.36 + 0.16) = 0.31

你可能就需要多观测几次，直到对当前的状态有一个比较准确的估计。

当然，这个例子过于简单，我们假定了当前的状态是固定的：老虎不会移动。一旦系统的状态会改变，例如我们预测气温的变化，一辆汽车的位置，就需要 g-h 滤波器 (Filter) 来动态地更新自己的估计了。

g-h Filter

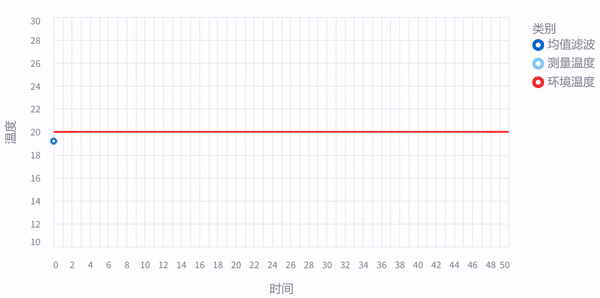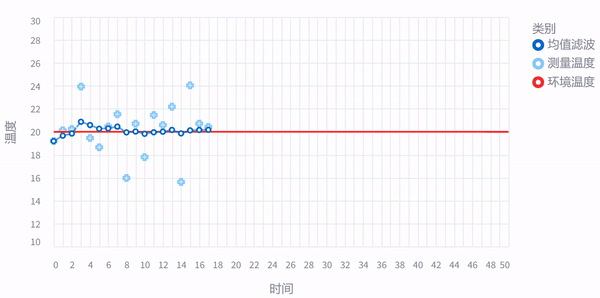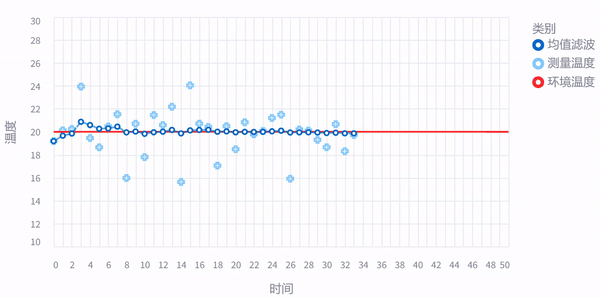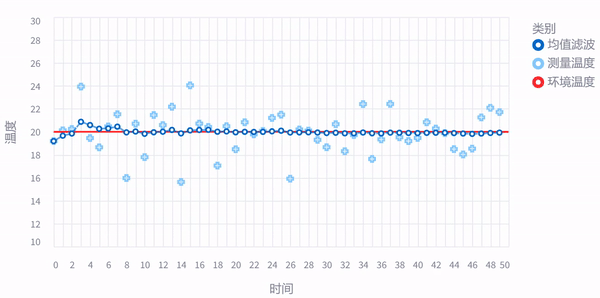
前面老虎的例子，主要是为了体现反复观测 (measurement) 的重要性，这样传感器 (sensor) 即使有测量误差，我们也可以通过反复测量，越来越接近真实值。比如下面这张图，假如房间温度几乎稳定不变，我们连续采样50次取平均值，哪怕测量值一直在抖动，最后我们计算的平均值几乎和房间实际温度一样了，这就是传说中的均值滤波。

那么问题来了，现实世界是一个动态的过程，面对一个反复横跳的老虎，或者正在加热的水壶，我们测量是需要花时间的，每次测量完，老虎的位置、或者水温就变了，那我们要怎么 动态地 追踪老虎的位置或者水温呢？

滤波的两个重要组成：预测 (Prediction) 和测量 (Measurement)

一种解决办法是 加强测量，例如之前文章提到的 互补滤波器 (Complementary Filter)，我们可以多放几个传感器，这样同一时间有好几个传感器的数据，把它们测量数据以一定比例结合起来，就比一个传感器精确多了。
另一种解决办法是 加强预测，毕竟我们也不能盲目相信传感器，测量再多次也都是有噪声的，于是我们需要引入物理模型，大概预测未来可能的测量值。比如老虎会横跳，但不会瞬间移动（至少现在的科技不太行），所以 $x = vt$ ，路程=速度*时间，我们大概就可以预测老虎未来可能的位置了。

再比如下面这张图，每一个点代表一个温度测量值，虽然传感器噪声很大，但是我们大致可以看出来温度是线性升高的，这样我们就可以用一个线性模型来大致预测下一秒温度范围了。

老虎的例子突出测量 (Measurement)，接下来突出预测 (Prediction)，这样滤波的两个核心就完整了。

现在开始正式介绍 g-h 滤波的算法了，这里先给出完整算法，其实就三行：

\begin{aligned} Step 1 (Prediction) & : {\tilde{x}}_{t + 1} = \hat{x_{t}} + v_{t} * Δ t \\ Step 2 (Update Position) & : {\hat{x}}_{t + 1} = {\tilde{x}}_{t + 1} + g * (z_{t + 1} - {\tilde{x}}_{t + 1}) \\ Step 2 (Update Velosity) & : v_{t + 1} = v_{t} + h * \frac{(z_{t + 1} - {\tilde{x}}_{t + 1})}{Δ t} \end{aligned}

$\begin{align} \text{Step 1 (Prediction)}&: \tilde{x}_{t+1}=\hat{x_t}+v_{t}*\Delta t\\ \\ \text{Step 2 (Update Position)}&: \hat{x}_{t+1}=\tilde{x}_{t+1}+g*({z_{t+1} - \tilde{x}_{t+1}}) \\ \text{Step 2 (Update Velosity)}&: v_{t+1} = v_{t} + h * \frac{({z_{t+1} - \tilde{x}_{t+1}})}{\Delta t}\\ \end{align}$
如果看不懂，别急，接下来会拆开来一步步解释。

第一步：预测 (Prediction)

首先，高中物理知识，我们可以通过当前时刻温度 $x_{t}$ ，和上一个时刻的温度 $x_{t-1}$ ，计算出来变化速度 $v$ ：

v = \frac{x_{t} - x_{t - 1}}{Δ t}

$v=\frac{x_{t} - x_{t-1}}{\Delta t}$

这样还可以推算出来，下一个时刻的温度 $x_{t+1}$ ：

x_{t + 1} = x_{t} + v_{t} * Δ t

$x_{t+1}=x_{t} + v_t*{\Delta t}$

这也就是前面提到的，g-h 滤波引入的物理预测模型，是不是非常简单。

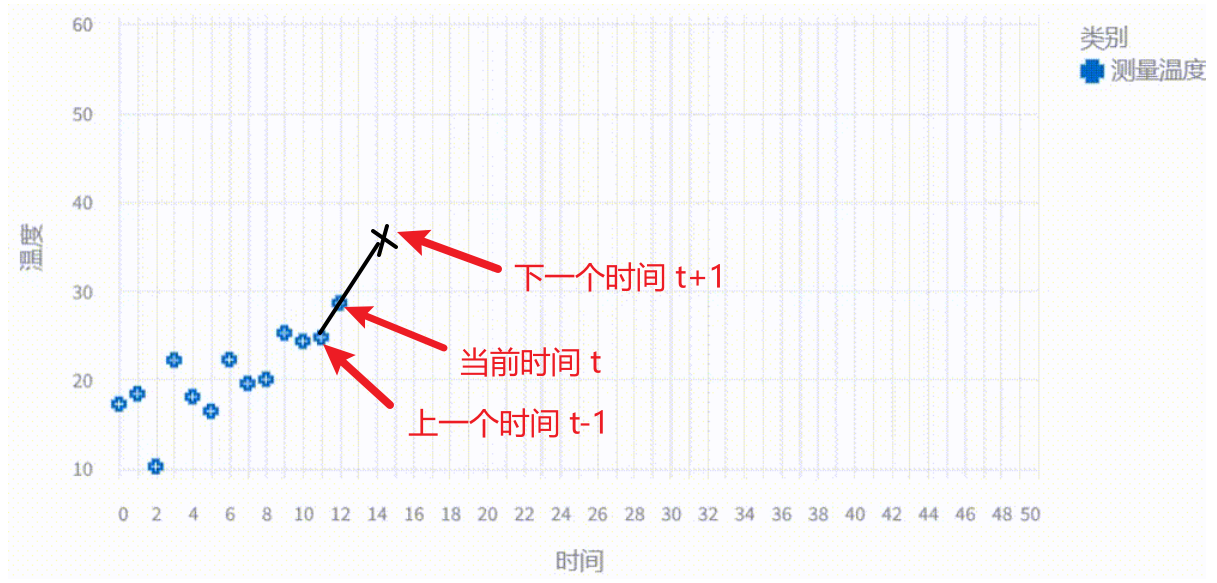
第一步的公式是不是就能看懂了，如果我们知道当前时刻估计的温度 $\hat{x}_t$ ，就能根据速度 $v_t$ 来算出下一时刻的预测值 $\tilde{x}_{t+1}$ 。

\begin{aligned} Step 1 (Prediction) & : {\tilde{x}}_{t + 1} = \hat{x_{t}} + v_{t} * Δ t \end{aligned}

$\begin{align} \text{Step 1 (Prediction)}&: \tilde{x}_{t+1}=\hat{x_t}+v_{t}*\Delta t \end{align}$
这里需要注意的是，

{\tilde{x}}_{t + 1}

$\tilde{x}_{t+1}$ 是模型预测值 (Prediction)，

x

$x$ 上面是个波浪号，然而物理模型的预测并不一定和实际吻合，所以我们还需要第二步，把模型预测值和实际测量值结合起来，得到滤波器最后的输出：估计值 (estimation)

{\hat{x}}_{t + 1}

$\hat{x}_{t+1}$ ，这里

x

$x$ 上面是小三角。

$\tilde{x}$ 读作 $x$ tilder，代表模型预测值； $\hat{x}$ 读作 $x$ hat，代表预测和测量结合，最终给出的估计值。

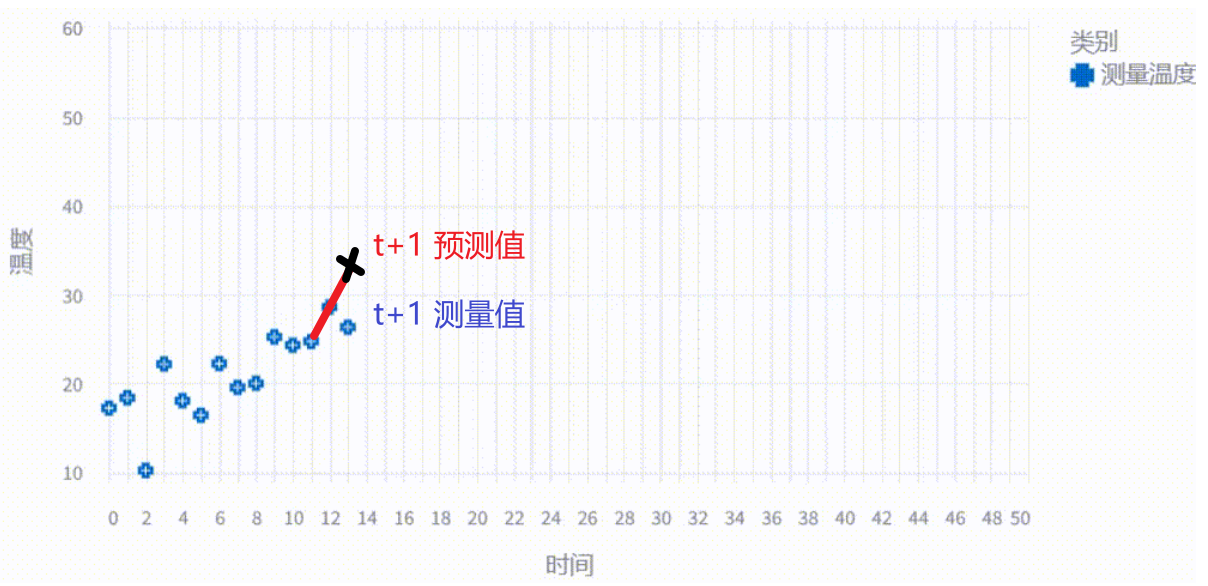
第二步：更新位置 (Update) - 参数 g

那么，我们怎么计算最终的估计值 $\hat{x}_{t+1}$ 呢？

其实很简单，我们现在手上有物理模型的预测值 $\tilde{x}_{t+1}$ 和实际测量值 $z_{t+1}$ ，只需要像互补滤波器那样按比例组合就可以了。

\begin{aligned} {\hat{x}}_{t + 1} & = (1 - g) * {\tilde{x}}_{t + 1} + g * z_{t + 1} \\ 估 计 值 & = (1 - g) * 模 型 预 测 + g * 测 量 值 \end{aligned}

$\begin{align} \hat{x}_{t+1} &= (1-g)*\tilde{x}_{t+1} + g*z_{t+1} \\ \\ 估计值 &= (1-g) * 模型预测 + g * 测量值 \end{align}$

这简直就和互补滤波器一模一样，只不过互补滤波器结合的是两个传感器数据，而 g-h 滤波器结合的是模型预测值，和实际测量值。

当 $g=0$ 的时候， $\hat{x}_{t+1}=\tilde{x}_{t+1}$ ，估计值=预测值，我们完全相信物理模型的预测值，直接忽略测量值；
当 $g=1$ 的时候， $\hat{x}_{t+1}=z_{t+1}$ ，估计值=测量值，我们完全相信下一个时刻的测量值，忽略物理模型。
当 $g$ 在 (0, 1) 之间的时候，我们结合物理模型和测量值，得到更准确的结果。

当然，为了区分 g-h 滤波和互补滤波器，有人也喜欢把公式换个形式：

\begin{aligned} {\hat{x}}_{t + 1} & = (1 - g) * {\tilde{x}}_{t + 1} + g * z_{t + 1} \\ = {\tilde{x}}_{t + 1} - g * {\tilde{x}}_{t + 1} + g * z_{t + 1} \\ = {\tilde{x}}_{t + 1} + g * (z_{t + 1} - {\tilde{x}}_{t + 1}) \\ 估 计 值 & = 模 型 预 测 + g * (测 量 值 - 模 型 预 测) \end{aligned}

$\begin{align} \hat{x}_{t+1} &= (1-g)*\tilde{x}_{t+1} + g*z_{t+1}\\ &= \tilde{x}_{t+1} - g*\tilde{x}_{t+1} + g*z_{t+1} \\ &= \tilde{x}_{t+1} + g*(z_{t+1} - \tilde{x}_{t+1}) \\ \\ 估计值 &= 模型预测 + g*(测量值-模型预测) \end{align}$

这样看起来更清爽，测量值和模型预测会有偏差： $g=0$ ，就不考虑偏差，相信预测； $g=1$ ，就记入全部偏差，相信测量。

相信 g-h 滤波器的第二步公式，你也能很轻松理解了：

\begin{aligned} Step 2 (Update Position) & : {\hat{x}}_{t + 1} = {\tilde{x}}_{t + 1} + g * (z_{t + 1} - {\tilde{x}}_{t + 1}) \end{aligned}

$\begin{align} \text{Step 2 (Update Position)}&: \hat{x}_{t+1}=\tilde{x}_{t+1}+g*({z_{t+1} - \tilde{x}_{t+1}}) \end{align}$

你可能说到这里 g-h 滤波器不就结束了吗？滤波器的估计值 $\hat x_{t+1}$ 已经算出来了呀，怎么还有个参数 $h$ 呢？

第二步：更新速度 (Update) - 参数 h

不知道你还记不记得，前面我们模型是根据变化速度 $v$ 来给出预测的，然而 $v$ 是动态变化的，我们还没有更新速度呢。

\begin{aligned} Step 2 (Update Velosity) & : v_{t + 1} = v_{t} + h * \frac{(z_{t + 1} - {\tilde{x}}_{t + 1})}{Δ t} \end{aligned}

$\begin{align} \text{Step 2 (Update Velosity)}&: v_{t+1} = v_{t} + h * \frac{({z_{t+1} - \tilde{x}_{t+1}})}{\Delta t} \end{align}$
这里的系数

h

$h$ 其实就是调整速度的更新，如果测量值

z_{t + 1}

$z_{t+1}$ 和模型预测

{\tilde{x}}_{t + 1}

$\tilde{x}_{t+1}$ 不一样，说明速度可能变了，我们要赶紧更新速度：

$h=0$ 我们就不更新速度，认为系统速度不变；
$h \neq 0$ 如果我们认为系统速度变化很大，例如反复横跳的老虎，就把 $h$ 设置大些；如果我们认为系统速度变化不大，比如行驶的火车一般不会急加速、急停， $h$ 就可以小一些。

到这里，g-h 滤波器的三个公式，你应该都能理解了：

\begin{aligned} Step 1 (Prediction) & : {\tilde{x}}_{t + 1} = \hat{x_{t}} + v_{t} * Δ t \\ Step 2 (Update Position) & : {\hat{x}}_{t + 1} = {\tilde{x}}_{t + 1} + g * (z_{t + 1} - {\tilde{x}}_{t + 1}) \\ Step 2 (Update Velosity) & : v_{t + 1} = v_{t} + h * \frac{(z_{t + 1} - {\tilde{x}}_{t + 1})}{Δ t} \end{aligned}

g

$g$ 和

h

$h$ 参数的大小呢？

g-h 参数选择

文章开头的时候，我说 $g-h$ 滤波器和 PID 控制很像，现在你应该理解了，毕竟 $g$ 和 $h$ 分别代表位置和速度，刚好类似比例系数 P 和微分系数 D，并且 PID 控制的乐趣就在于调参，接下来我会介绍怎么调节 $g$ 和 $h$ 。

这里你可能灵光一闪，我们没有考虑加速度啊？恭喜你如果早出生几年， $\alpha-\beta-\gamma$ 滤波器就是你提出来的了。

假设我们加热水壶，水温先逐渐上升，最后几乎稳定不变，我们要怎么调节 $g-h$ 参数去动态估计水温呢？

情况1：g=0, h=0 (完全相信模型，速度不变)

首先，我们看一下如果 $g=0$ ， $h=0$ ，那 $g-h$ 滤波器会画出怎样的估计曲线呢？

\begin{aligned} Step 2 (Update Position) & : {\hat{x}}_{t + 1} = {\tilde{x}}_{t + 1} + 0 * (z_{t + 1} - {\tilde{x}}_{t + 1}) \\ Step 2 (Update Velosity) & : v_{t + 1} = v_{t} + 0 * \frac{(z_{t + 1} - {\tilde{x}}_{t + 1})}{Δ t} \end{aligned}

$\begin{align} \text{Step 2 (Update Position)}&: \hat{x}_{t+1}=\tilde{x}_{t+1}+0*({z_{t+1} - \tilde{x}_{t+1}}) \\ \text{Step 2 (Update Velosity)}&: v_{t+1} = v_{t} + 0 * \frac{({z_{t+1} - \tilde{x}_{t+1}})}{\Delta t}\\ \end{align}$

你也可以先根据公式，自己思考。我故意放公式和大图在这里，答案在这下面。

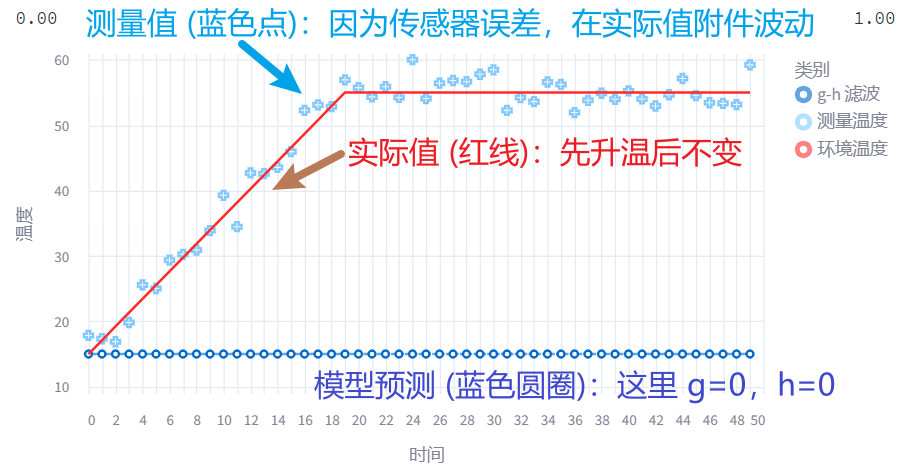
经过思考，不知道你是不是得出和我一样的结论， $g-h$ 滤波器会画出一条直线。

g=0，说明我们完全相信模型预测值，完全不考虑传感器的测量值；
h=0，说明我们认为系统速度不变，也就是水温改变速度始终和最开始一样，由于最开始 $t=0$ 的时候，我们不知道速度，只能设置 $v_0=0$ ，后面 $v_{t+1}=v_{t}=v_0=0$ 于是水温一直不变。

最终， $g-h$ 不管传感器测量结果是多少，都估计水温和最开始一样不变，就画出了一条直线。

这里顺便一提，除了初始速度 $v_0=0$ ， $g-h$ 滤波器需要你指定一个初始值 $x_0$ ，也就是最初的水温。如果你知道初始值当然最好，不知道的话 $x_0=0$ 就行了，后面 $g-h$ 滤波器会根据测量值，逐渐逼近真实水温的。

情况2：g=0, h≠0 (完全相信模型，改变速度)

如果我们还是相信模型 $g=0$ ，但是 $h \neq 0$ 呢？

\begin{aligned} Step 2 (Update Position) & : {\hat{x}}_{t + 1} = {\tilde{x}}_{t + 1} + 0 * (z_{t + 1} - {\tilde{x}}_{t + 1}) = z_{t + 1} \\ Step 2 (Update Velosity) & : v_{t + 1} = v_{t} + h * \frac{(z_{t + 1} - {\tilde{x}}_{t + 1})}{Δ t} \end{aligned}

$\begin{align} \text{Step 2 (Update Position)}&: \hat{x}_{t+1}=\tilde{x}_{t+1}+0*({z_{t+1} - \tilde{x}_{t+1}}) = z_{t+1} \\ \text{Step 2 (Update Velosity)}&: v_{t+1} = v_{t} + h * \frac{({z_{t+1} - \tilde{x}_{t+1}})}{\Delta t}\\ \end{align}$

$g=0$ 说明我们完全相信模型预测，根本不受测量值的影响；
$h \neq 0$ 调整的是模型的速度更新快慢，由于我们完全相信模型预测， $h$ 就很重要了。

现在我们固定 $g=0$ ，把 $h$ 由小逐渐增大看看效果。

$h=0.06$ 的时候，速度更新非常缓慢，后面温度不变了， $g-h$ 滤波器的速度调节太慢，出了一个缓慢调节的正弦曲线。

2024_10_21_12_09_15_669.mp4 [video-to-gif output image]

$h=0.8$ 的时候，速度又更新太快了，导致滤波器输出反复震荡，画出了一个高频震荡曲线。

2024_10_21_12_14_34_346.mp4 [video-to-gif output image]

所以当你的滤波器震荡的时候，可能就是 $h$ 的范围没有设置好了，这也非常类似 PID 控制的微分项 D。

情况3：g=1, h≠0 (完全相信传感器)

同样，你也可以先自己思考一下：

\begin{aligned} Step 2 (Update Position) & : {\hat{x}}_{t + 1} = {\tilde{x}}_{t + 1} + 1 * (z_{t + 1} - {\tilde{x}}_{t + 1}) = z_{t + 1} \\ Step 2 (Update Velosity) & : v_{t + 1} = v_{t} + h * \frac{(z_{t + 1} - {\tilde{x}}_{t + 1})}{Δ t} \end{aligned}

$\begin{align} \text{Step 2 (Update Position)}&: \hat{x}_{t+1}=\tilde{x}_{t+1}+1*({z_{t+1} - \tilde{x}_{t+1}}) = z_{t+1} \\ \text{Step 2 (Update Velosity)}&: v_{t+1} = v_{t} + h * \frac{({z_{t+1} - \tilde{x}_{t+1}})}{\Delta t}\\ \end{align}$

$g=1$ 说明我们完全相信测量值，根本不受模型预测的影响；
$h \neq 0$ 调整的是模型的速度更新快慢，然而 $g=1$ 不考虑模型了，说明我们无论怎么调节 $h$ 都没区别。

可以从下面的动画看到，无论我怎么调节 $h$ ，滤波器给出的估计 (蓝色圈圈) 和测量值始终一模一样。

2024_10_21_11_58_11_484.mp4 [speed output image]

情况4: g=0.39, h≠0.01 (结合模型和传感器)

现在你应该感受到 $g-h$ 参数调节的重要性，在经过多次调节后，才能找到比较合适的参数。

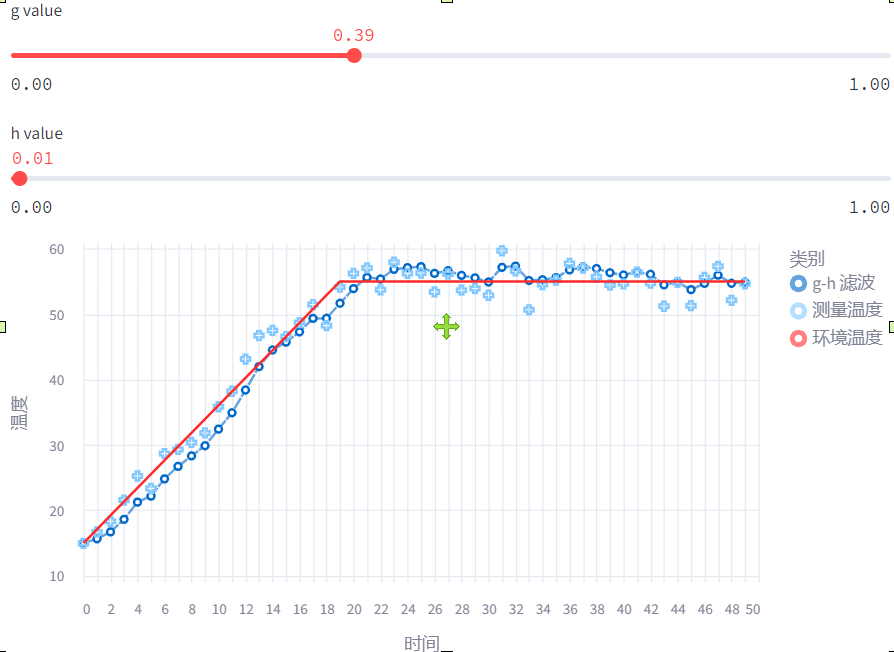
然而不幸的是，同一组参数并不能适用所有的系统，比如下面如果温度逐渐加速升高，可以看见同样的 $g-h$ 参数，我们的估计总是滞后实际的温度的。

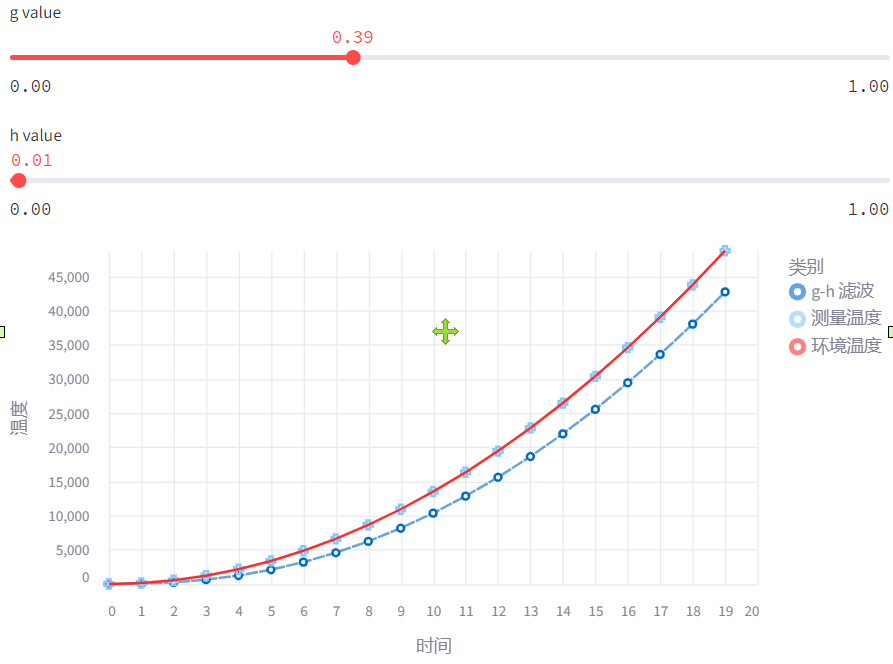
这里一方面是 $g-h$ 滤波器没有考虑加速度，你可以尝试升级 $\alpha-\beta-\gamma$ 滤波器，或者有没有什么办法能动态地调节 $g-h$ 参数呢？没错，这就诞生了大名鼎鼎的 Kalman Filter 了。

总结

最早，互补滤波器一行公式结合了2个传感器的数据。

后来， $g-h$ 滤波器用类似的公式，结合了物理模型和传感器数据，但是需要手动调节参数。

再后来，Kalman 滤波器自动调节参数，更加灵活。

如果你想自己体验调整 g-h 参数的乐趣，也可以在下面这个网站上尝试，文章里的动画其实就是录制的这个网站：

$g-h$ 滤波器演示网站：https://g-h.wuhanstudio.cc/
网站开源地址：https://github.com/wuhanstudio/g-h-filter

g-h 滤波器 与 PID 控制 (Filter & Control)

简介 滤波器 (Filter)