CNN 并没有用 卷积 (Convolution)
TL;DR: CNN uses cross-correlation, NOT convolution.
最近讲 CV Workshop 才意识到,原来 卷积神经网络 (CNN) 用的并不是 卷积 (Convolution),实际上用的是 Cross-Correlation。
Convolutional Neural Network (CNN) 实际上是 Cross-Correlation Neural Network (CCNN),可能大家习惯了,也懒得改了。

这篇文章会先介绍 Convolution 和 Cross-Correlation 的区别,为什么 深度学习 混淆了它们;接下来回到 信号处理,理解什么是 Convolution,为什么要计算 Convolution?公式右边的 积分为什么是
1 Convolution in Deep Learning
每当提到深度学习的卷积,很多人脑海里都会闪过这样一个小动画:
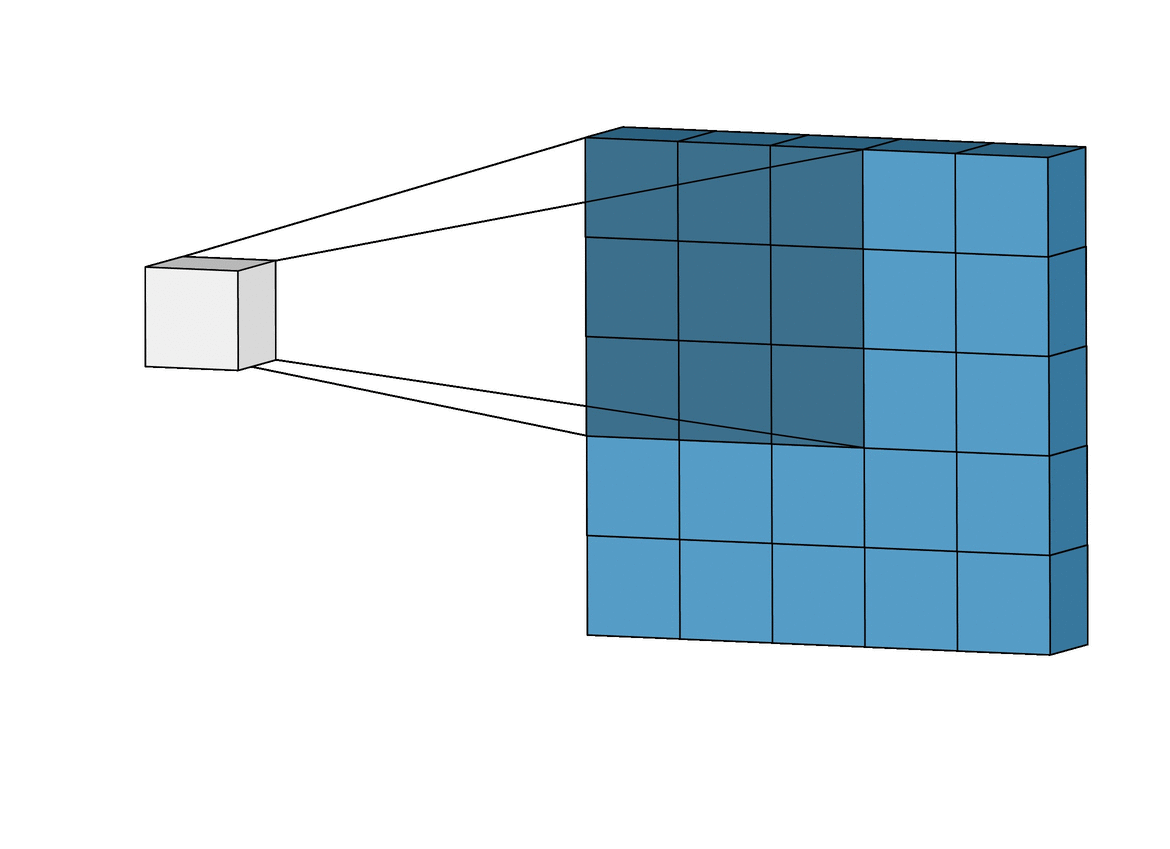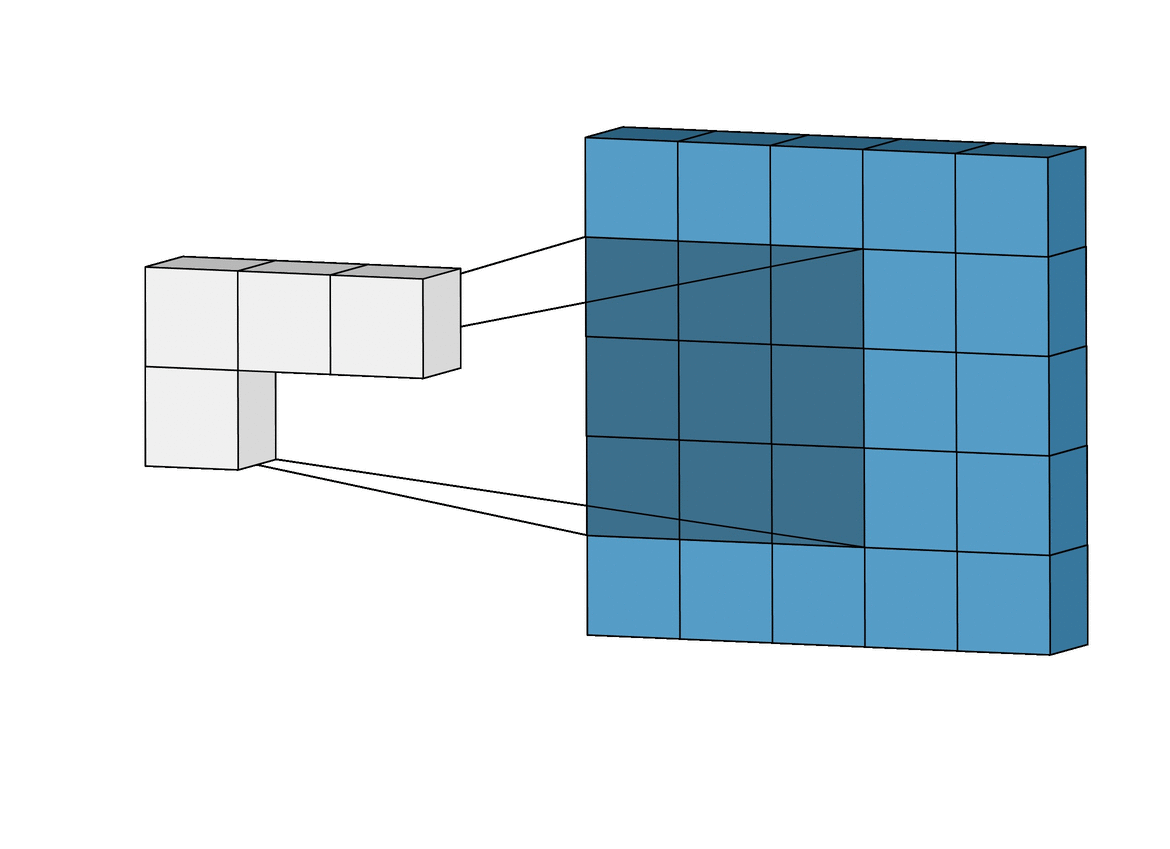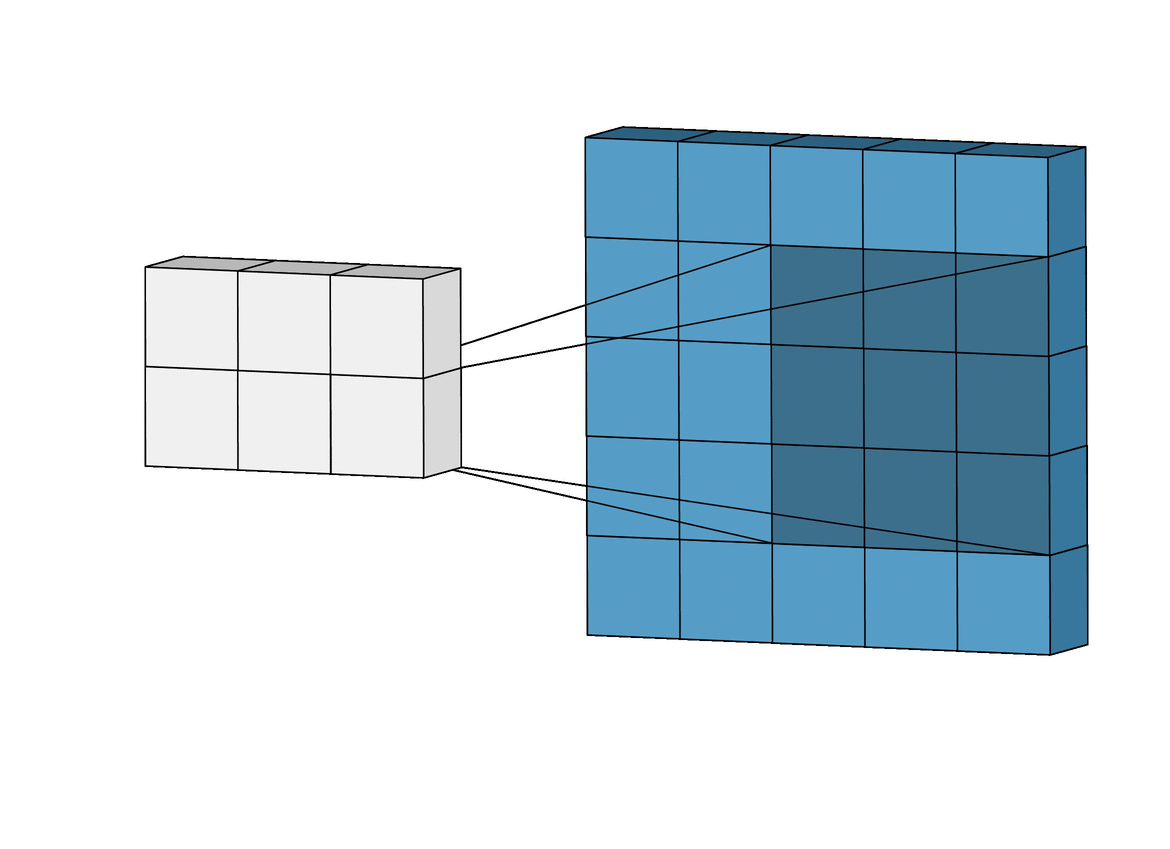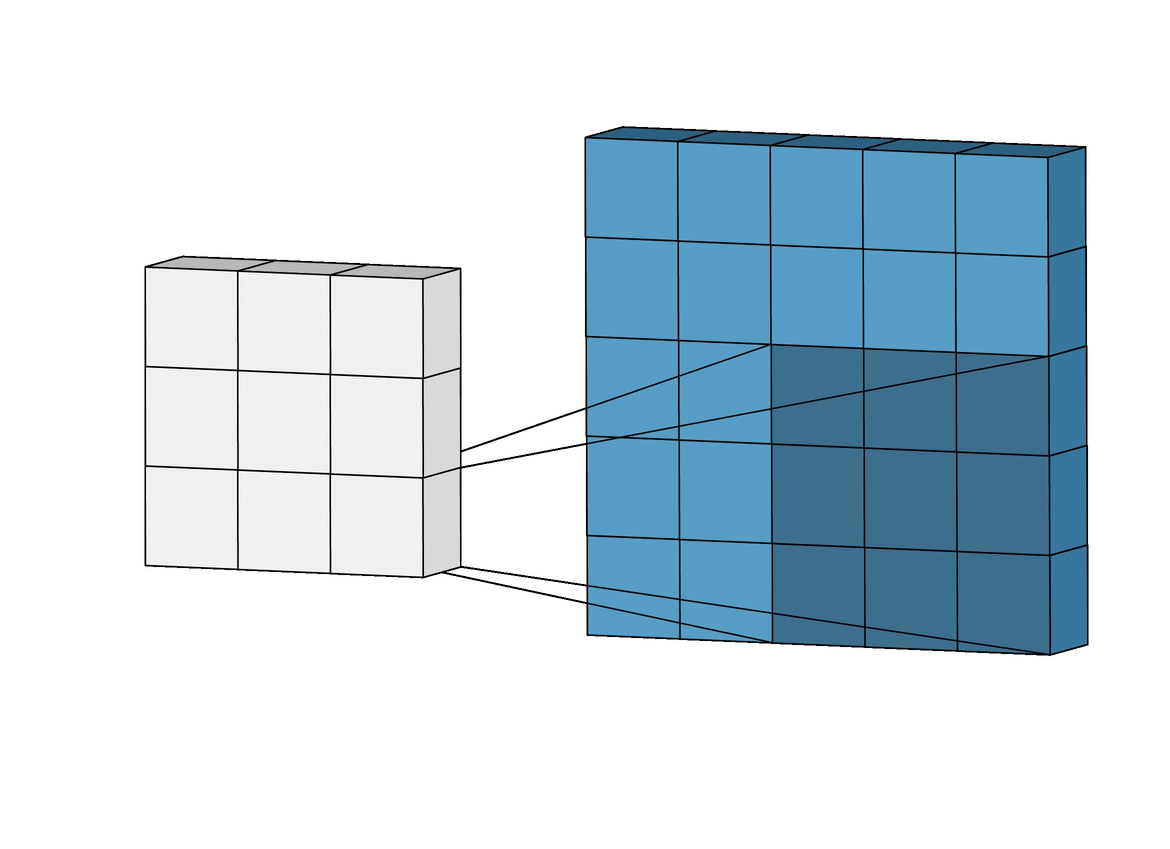
例如我们用一个 3x3 的 kernel 和一个图像做卷积,其实就是把这个 kernel 从左到右,从上到下扫过一张图片,然后对应位做乘法,最后相加求和就可以了:
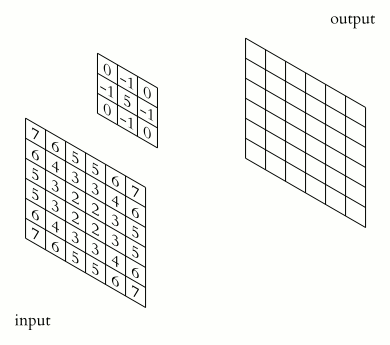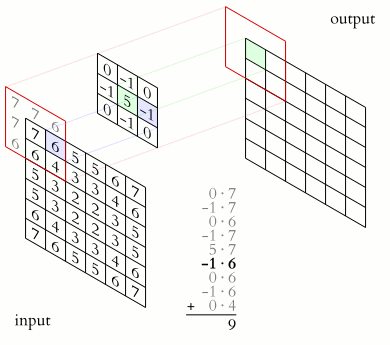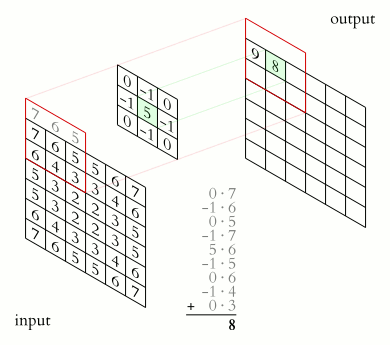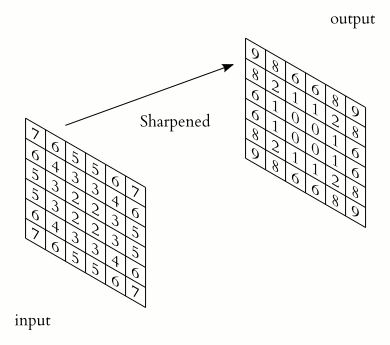
然而如果我们细看这个方法,就会发现 它其实并不是 Convolution (符号:
实际上,真正的卷积应当是这样计算的:
上面的公式是 element-wise 对应位相乘 (ax1, bx2, cx3 ...),而下面的公式则是把矩阵 先上下左右反转 之后,再对应位相乘的 (ax9, bx8, cx7 ...):
标准定义
如果我们用
上面 Cross-Correlation 是
信号处理
如果你以前学过 信号处理 (Signal Processing),可能恍然大悟,一个信号
于是 前面离散的
2 Convolution & Cross-Correlation
那么问题来了,为什么会犯这个错误呢?
最开始 Computer Vision 是把图像当作 2D 的信号处理的,所以借用了很多 Signal Processing 里的方法:
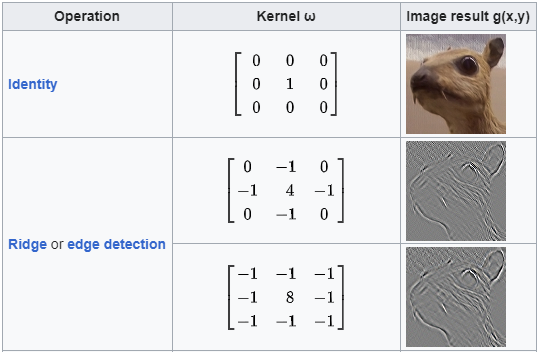
而在 Signal Processing 领域,很多 kernel filters 都是 对称函数,所以应用到 图像处理,很自然的用了 对称矩阵。
前面提到 Convolution 需要 上下左右反转矩阵,如果我们把上面的 对称矩阵 翻转会发现,还是原矩阵。
也就是说对一个 Symmetric Matrix 来讲,Convolution 和 Cross-Correlation 的计算结果是一样的,以至于 CNN 原作者可能没注意到两者的区别。
然而,深度学习里的 CNN 训练出来的 kernel 通常并不是 Symmetric,所以 CNN 计算的实际上是 Cross-Correlation,并不等同 Convolution,不过 CNN 都叫好多年了,也就这样了,懒得改了。
3 什么是 Convolution?
那么更多问题又来了,到底什么是 Convolution 呢?为什么要计算 Convolution 呢?
一个很有意思的例子,一个 Professor 早上骑自行车锻炼身体的时候,突然灵感一现,开始介绍什么是 Convolution,我也终于理解了以前本科为什么要学 Step Response 处理这种现实并不 单独常见 的信号。

如果我们骑自行车经过一条小路,路上坑坑洼洼会有一些小石头:

那么当自行车经过这些石头的时候,挤压轮胎,轮胎就会变型。但自行车轮胎并不是瞬间变形,又瞬间恢复的:也就是说轮胎还没恢复,可能又轧到后面的石头,进一步变形,最终轮胎的形变,是一系列石头压力的共同作用。

所以我们很自然地可以把石头离散,一个连续的石头施加的力,被离散成一系列细小的力,最后求积分,而每一个细小的力产生的变形,就是 Step Response,比如轮胎的响应一开始会有一个大的形变,最后随着时间的推移慢慢消失
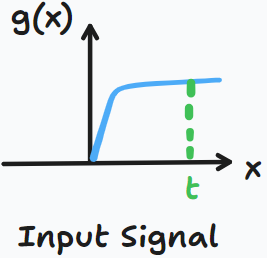
对于信号处理而言,路上的石头施加的力是 Input Signal
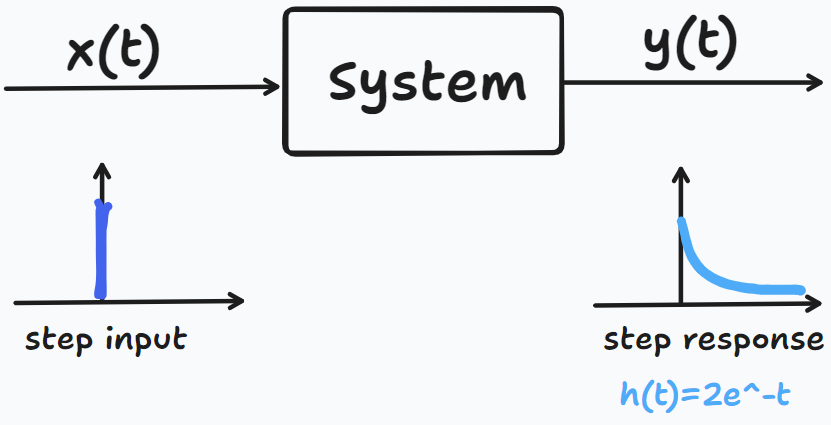
这个自行车轧过小石头的例子,就像 Convolution 一个信号扫过另一个信号,计算两个信号叠加面积的过程。
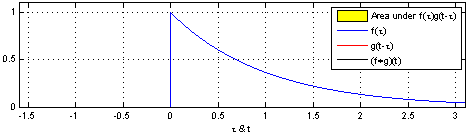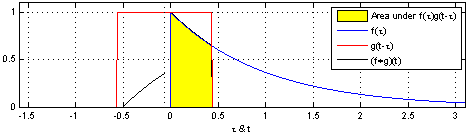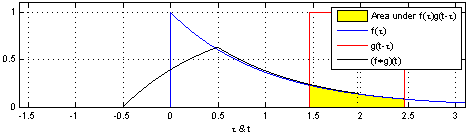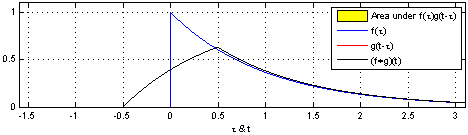
所以我们计算 Convolution 就是计算信号叠加的过程,如果我们知道系统的 Step Response
4 为什么计算 Convolution 要 翻转 信号?
首先,我们简化一下上面的公式。
实际的信号并不会从
这个时候我们在
另一方面,如果我们关心的是到
那么最后一个问题来了,也为什么积分项里面是
不是两个信号叠加吗,怎么是输入信号
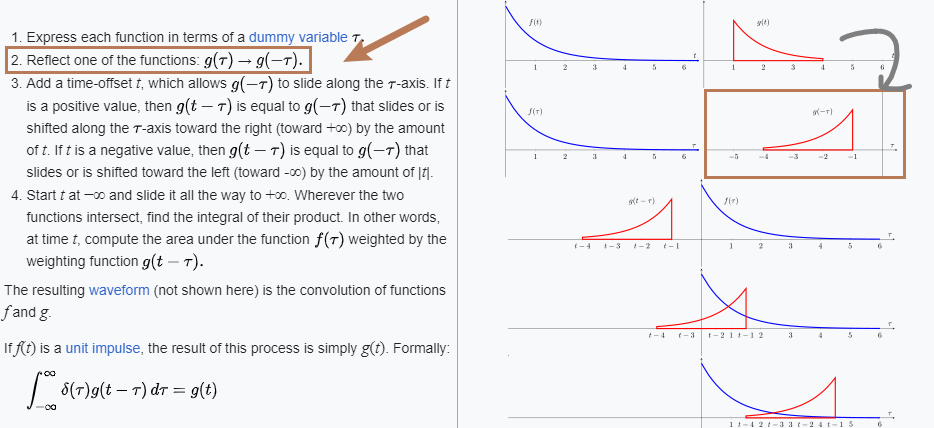
上面这张图可能是很多学 Signal Processing 的人牢记的公式,但是随着时间推移,却忘了为什么要翻转和平移信号。
其实原因很简单,我们在
总结
在一系列追根朔源的挖掘后,我终于理解为什么 CNN 把 Cross-Correlation 误当作了 Convolution,以及 Convolution 到底在计算什么,最后又是如何推导出经典的连续卷积公式:
这就是科研和讲课的乐趣,在给学生讲课的同时,逐渐补充了以前可能没有注意到的理论细节,对科研的深入也有很大帮助。